Action Redundancy in Reinforcement Learning
Paper and Code
Feb 22, 2021

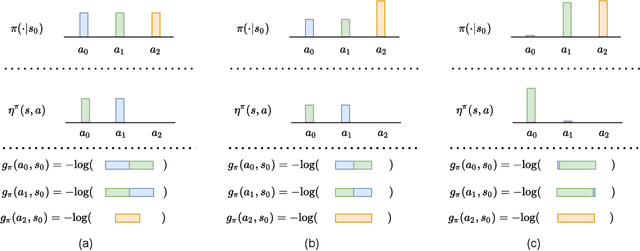

Maximum Entropy (MaxEnt) reinforcement learning is a powerful learning paradigm which seeks to maximize return under entropy regularization. However, action entropy does not necessarily coincide with state entropy, e.g., when multiple actions produce the same transition. Instead, we propose to maximize the transition entropy, i.e., the entropy of next states. We show that transition entropy can be described by two terms; namely, model-dependent transition entropy and action redundancy. Particularly, we explore the latter in both deterministic and stochastic settings and develop tractable approximation methods in a near model-free setup. We construct algorithms to minimize action redundancy and demonstrate their effectiveness on a synthetic environment with multiple redundant actions as well as contemporary benchmarks in Atari and Mujoco. Our results suggest that action redundancy is a fundamental problem in reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge