Achieving O(1/N) Optimality Gap in Restless Bandits through Diffusion Approximation

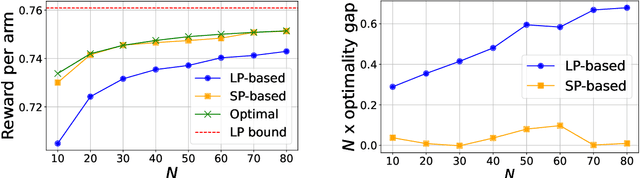
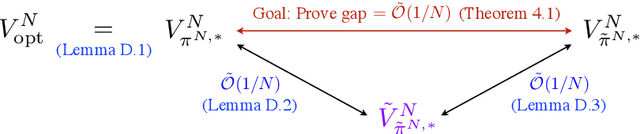
We study the finite horizon Restless Multi-Armed Bandit (RMAB) problem with $N$ homogeneous arms, focusing on the challenges posed by degenerate RMABs, which are prevalent in practical applications. While previous work has shown that Linear Programming (LP)-based policies achieve exponentially fast convergence relative to the LP upper bound in non-degenerate models, applying these LP-based policies to degenerate RMABs results in slower convergence rates of $O(1/\sqrt{N})$. We construct a diffusion system that incorporates both the mean and variance of the stochastic processes, in contrast to the fluid system from the LP, which only accounts for the mean, thereby providing a more accurate representation of RMAB dynamics. Consequently, our novel diffusion-resolving policy achieves an optimality gap of $O(1/N)$ relative to the true optimal value, rather than the LP upper bound, revealing that the fluid approximation and the LP upper bound are too loose in degenerate settings. These insights pave the way for constructing policies that surpass the $O(1/\sqrt{N})$ optimality gap for any RMAB, whether degenerate or not.