Achieving differential privacy for $k$-nearest neighbors based outlier detection by data partitioning
Paper and Code
Apr 16, 2021


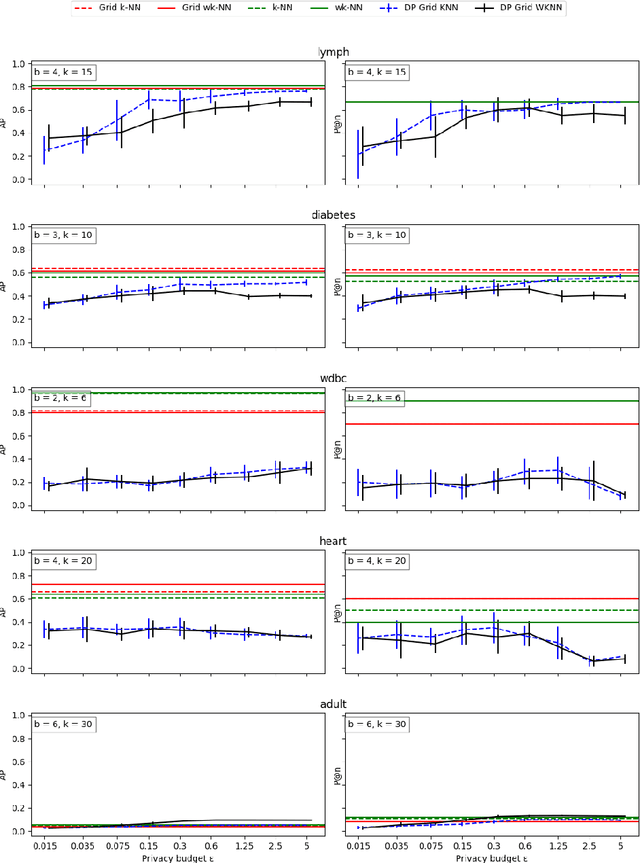
When applying outlier detection in settings where data is sensitive, mechanisms which guarantee the privacy of the underlying data are needed. The $k$-nearest neighbors ($k$-NN) algorithm is a simple and one of the most effective methods for outlier detection. So far, there have been no attempts made to develop a differentially private ($\epsilon$-DP) approach for $k$-NN based outlier detection. Existing approaches often relax the notion of $\epsilon$-DP and employ other methods than $k$-NN. We propose a method for $k$-NN based outlier detection by separating the procedure into a fitting step on reference inlier data and then apply the outlier classifier to new data. We achieve $\epsilon$-DP for both the fitting algorithm and the outlier classifier with respect to the reference data by partitioning the dataset into a uniform grid, which yields low global sensitivity. Our approach yields nearly optimal performance on real-world data with varying dimensions when compared to the non-private versions of $k$-NN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge