Accelerating Monte Carlo Bayesian Inference via Approximating Predictive Uncertainty over Simplex
Paper and Code
May 29, 2019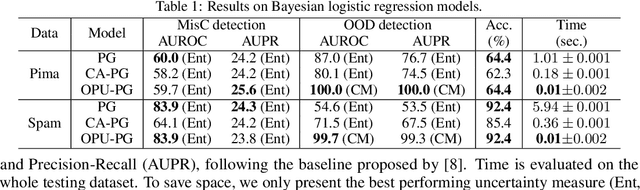
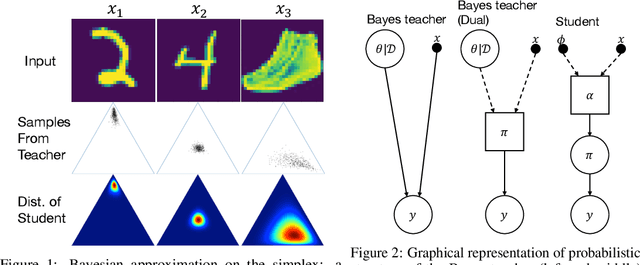
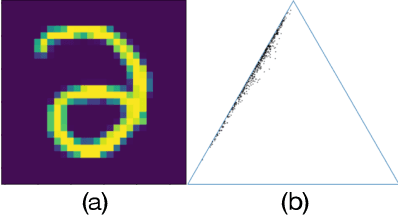
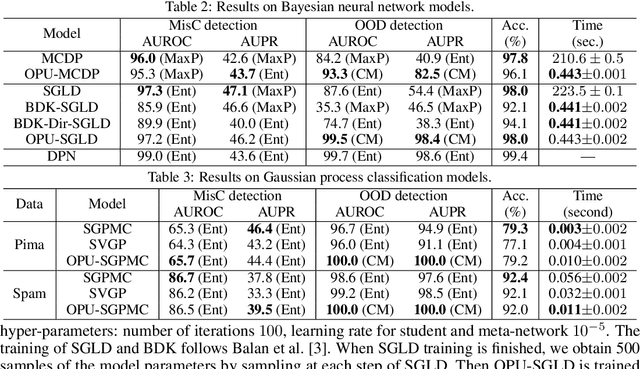
Estimating the uncertainty of a Bayesian model has been investigated for decades. The model posterior is almost always intractable, such that approximation is necessary. In many real-world cases, even though a decent estimation of the model posterior is obtained, another approximation is required to compute the predictive distribution over the desired output. A common accurate solution is to use Monte Carlo (MC) integration. However, it needs to maintain a large number of samples, evaluate the model repeatedly and average multiple model outputs. In this paper, we propose a method to approximate the probability distribution over the simplex induced by model posterior, enabling tractable computation of the predictive distribution for classification. The aim is to approximate the induced uncertainty of a specific Bayesian model, meanwhile alleviating the heavy workload of MC integration in testing time. Methodologically, we adapt Wasserstein distance to learn the induced conditional distributions, which is novel for Bayesian learning. The proposed method is universally applicable to Bayesian classification models that allow for posterior sampling. Empirical results validate the strong practical performance of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge