Ab-Initio Potential Energy Surfaces by Pairing GNNs with Neural Wave Functions

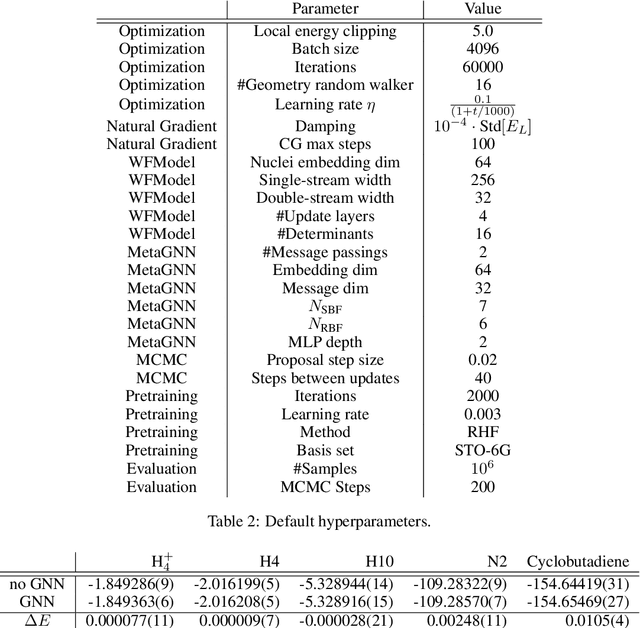
Solving the Schr\"odinger equation is key to many quantum mechanical properties. However, an analytical solution is only tractable for single-electron systems. Recently, neural networks succeeded at modelling wave functions of many-electron systems. Together with the variational Monte-Carlo (VMC) framework, this led to solutions on par with the best known classical methods. Still, these neural methods require tremendous amounts of computational resources as one has to train a separate model for each molecular geometry. In this work, we combine a Graph Neural Network (GNN) with a neural wave function to simultaneously solve the Schr\"odinger equation for multiple geometries via VMC. This enables us to model continuous subsets of the potential energy surface with a single training pass. Compared to existing state-of-the-art networks, our Potential Energy Surface Network (PESNet) speeds up training for multiple geometries by up to 40 times while matching or surpassing their accuracy. This may open the path to accurate and orders of magnitude cheaper quantum mechanical calculations.