A Wiener process perspective on local intrinsic dimension estimation methods
Paper and Code
Jun 24, 2024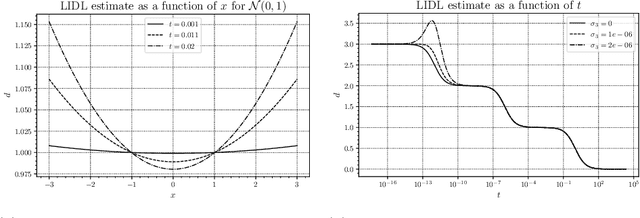
Local intrinsic dimension (LID) estimation methods have received a lot of attention in recent years thanks to the progress in deep neural networks and generative modeling. In opposition to old non-parametric methods, new methods use generative models to approximate diffused dataset density and scale the methods to high-dimensional datasets like images. In this paper, we investigate the recent state-of-the-art parametric LID estimation methods from the perspective of the Wiener process. We explore how these methods behave when their assumptions are not met. We give an extended mathematical description of those methods and their error as a function of the probability density of the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge