A Wasserstein Minimum Velocity Approach to Learning Unnormalized Models
Paper and Code
Feb 18, 2020
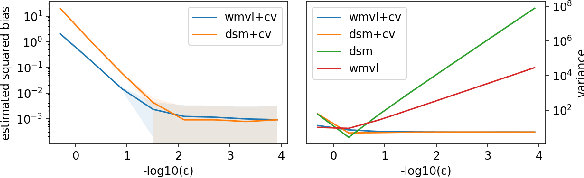
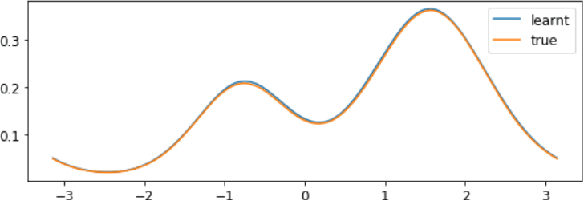
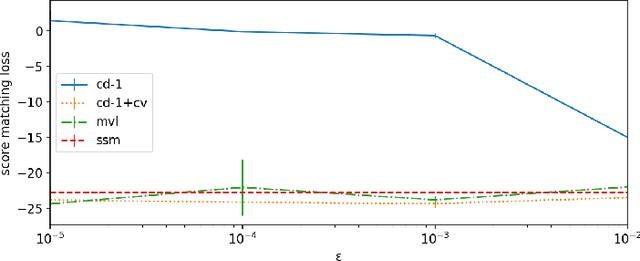
Score matching provides an effective approach to learning flexible unnormalized models, but its scalability is limited by the need to evaluate a second-order derivative. In this paper, we present a scalable approximation to a general family of learning objectives including score matching, by observing a new connection between these objectives and Wasserstein gradient flows. We present applications with promise in learning neural density estimators on manifolds, and training implicit variational and Wasserstein auto-encoders with a manifold-valued prior.
* AISTATS 2020
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge