A Unifying View on Implicit Bias in Training Linear Neural Networks

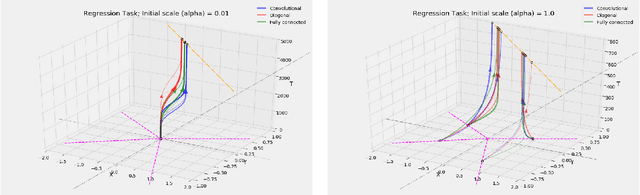
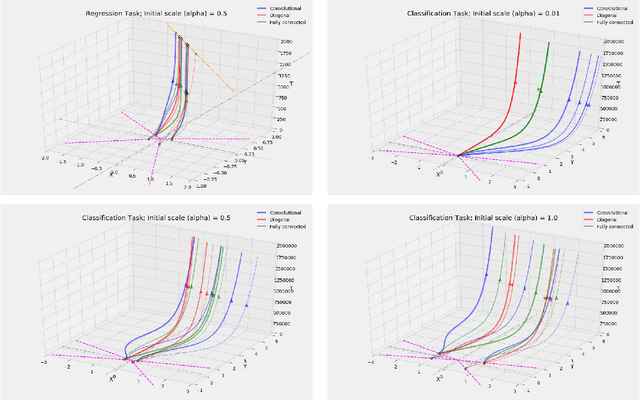
We study the implicit bias of gradient flow (i.e., gradient descent with infinitesimal step size) on linear neural network training. We propose a tensor formulation of neural networks that includes fully-connected, diagonal, and convolutional networks as special cases, and investigate the linear version of the formulation called linear tensor networks. For $L$-layer linear tensor networks that are orthogonally decomposable, we show that gradient flow on separable classification finds a stationary point of the $\ell_{2/L}$ max-margin problem in a "transformed" input space defined by the network. For underdetermined regression, we prove that gradient flow finds a global minimum which minimizes a norm-like function that interpolates between weighted $\ell_1$ and $\ell_2$ norms in the transformed input space. Our theorems subsume existing results in the literature while removing most of the convergence assumptions. We also provide experiments that corroborate our analysis.