A Transportation $L^p$ Distance for Signal Analysis
Paper and Code
Sep 27, 2016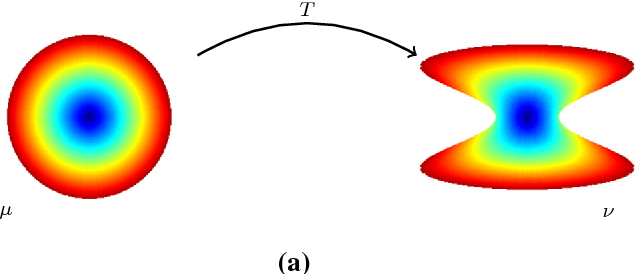
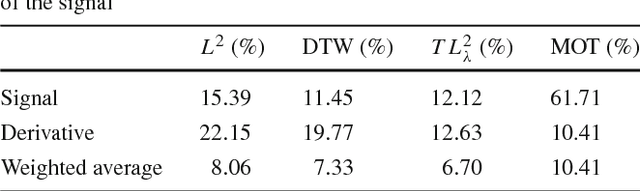
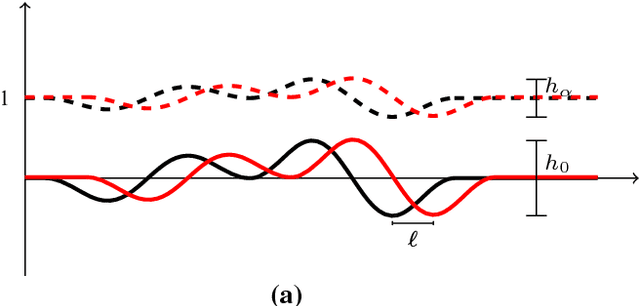
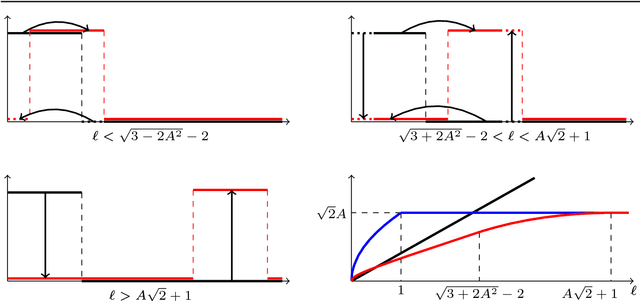
Transport based distances, such as the Wasserstein distance and earth mover's distance, have been shown to be an effective tool in signal and image analysis. The success of transport based distances is in part due to their Lagrangian nature which allows it to capture the important variations in many signal classes. However these distances require the signal to be nonnegative and normalized. Furthermore, the signals are considered as measures and compared by redistributing (transporting) them, which does not directly take into account the signal intensity. Here we study a transport-based distance, called the $TL^p$ distance, that combines Lagrangian and intensity modelling and is directly applicable to general, non-positive and multi-channelled signals. The framework allows the application of existing numerical methods. We give an overview of the basic properties of this distance and applications to classification, with multi-channelled, non-positive one and two-dimensional signals, and color transfer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge