A study of local optima for learning feature interactions using neural networks
Paper and Code
Feb 11, 2020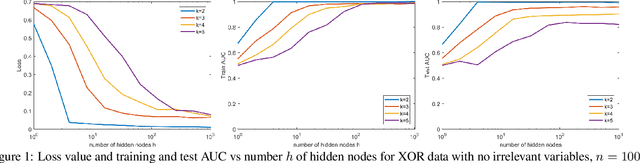
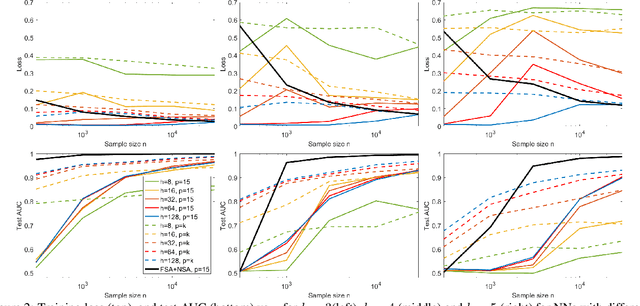
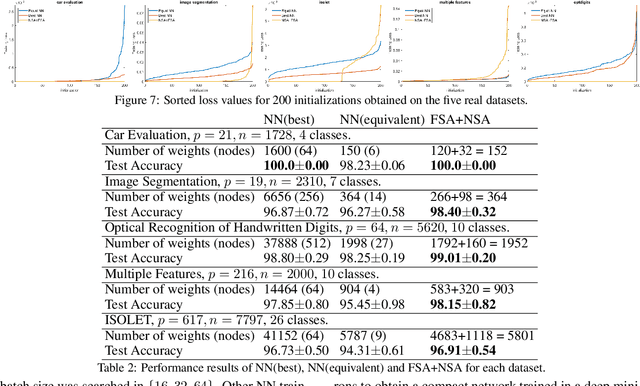
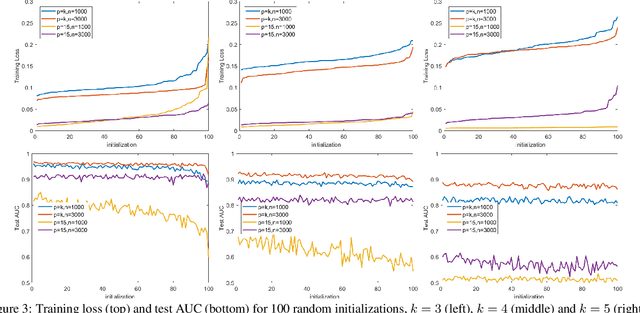
In many fields such as bioinformatics, high energy physics, power distribution, etc., it is desirable to learn non-linear models where a small number of variables are selected and the interaction between them is explicitly modeled to predict the response. In principle, neural networks (NNs) could accomplish this task since they can model non-linear feature interactions very well. However, NNs require large amounts of training data to have a good generalization. In this paper we study the datastarved regime where a NN is trained on a relatively small amount of training data. For that purpose we study feature selection for NNs, which is known to improve generalization for linear models. As an extreme case of data with feature selection and feature interactions we study the XOR-like data with irrelevant variables. We experimentally observed that the cross-entropy loss function on XOR-like data has many non-equivalent local optima, and the number of local optima grows exponentially with the number of irrelevant variables. To deal with the local minima and for feature selection we propose a node pruning and feature selection algorithm that improves the capability of NNs to find better local minima even when there are irrelevant variables. Finally, we show that the performance of a NN on real datasets can be improved using pruning, obtaining compact networks on a small number of features, with good prediction and interpretability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge