A simple geometric proof for the benefit of depth in ReLU networks

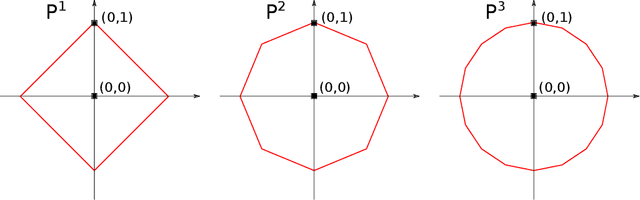
We present a simple proof for the benefit of depth in multi-layer feedforward network with rectified activation ("depth separation"). Specifically we present a sequence of classification problems indexed by $m$ such that (a) for any fixed depth rectified network there exist an $m$ above which classifying problem $m$ correctly requires exponential number of parameters (in $m$); and (b) for any problem in the sequence, we present a concrete neural network with linear depth (in $m$) and small constant width ($\leq 4$) that classifies the problem with zero error. The constructive proof is based on geometric arguments and a space folding construction. While stronger bounds and results exist, our proof uses substantially simpler tools and techniques, and should be accessible to undergraduate students in computer science and people with similar backgrounds.