A similarity-based Bayesian mixture-of-experts model

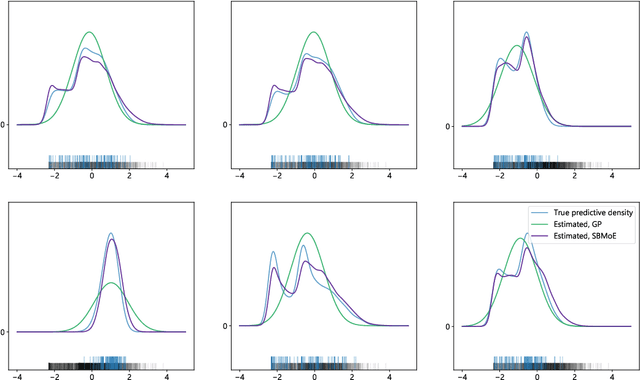
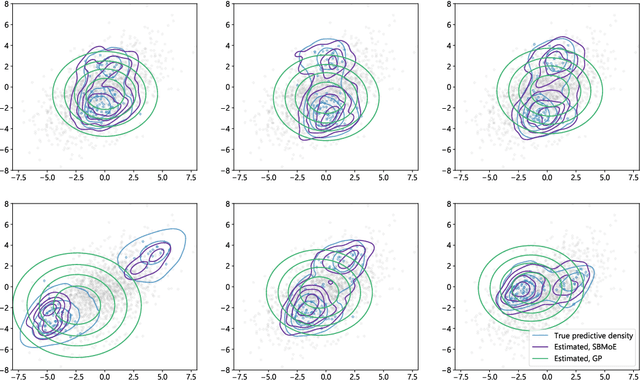
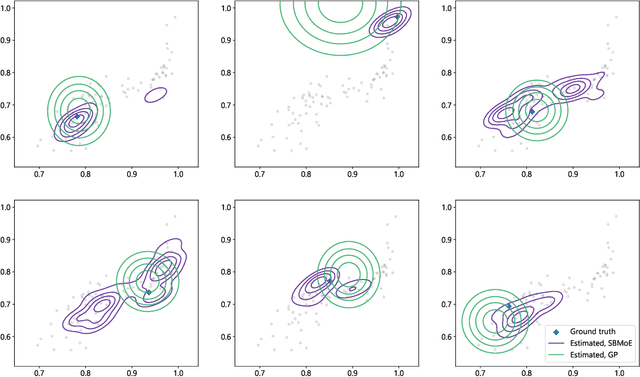
We present a new nonparametric mixture-of-experts model for multivariate regression problems, inspired by the probabilistic $k$-nearest neighbors algorithm. Using a conditionally specified model, predictions for out-of-sample inputs are based on similarities to each observed data point, yielding predictive distributions represented by Gaussian mixtures. Posterior inference is performed on the parameters of the mixture components as well as the distance metric using a mean-field variational Bayes algorithm accompanied with a stochastic gradient-based optimization procedure. The proposed method is especially advantageous in settings where inputs are of relatively high dimension in comparison to the data size, where input--output relationships are complex, and where predictive distributions may be skewed or multimodal. Computational studies on two synthetic datasets and one dataset comprising dose statistics of radiation therapy treatment plans show that our mixture-of-experts method outperforms a Gaussian process benchmark model both in terms of validation metrics and visual inspection.