A Semiparametric Instrumented Difference-in-Differences Approach to Policy Learning
Paper and Code
Oct 14, 2023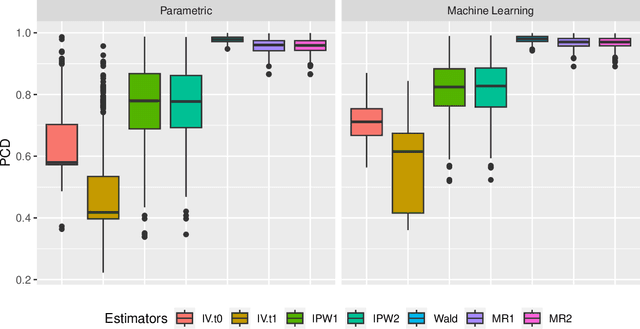
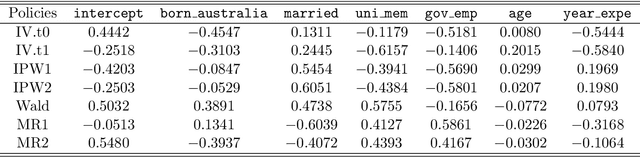
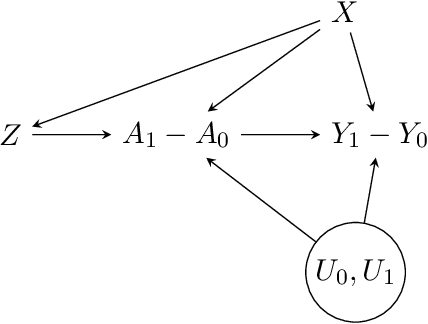
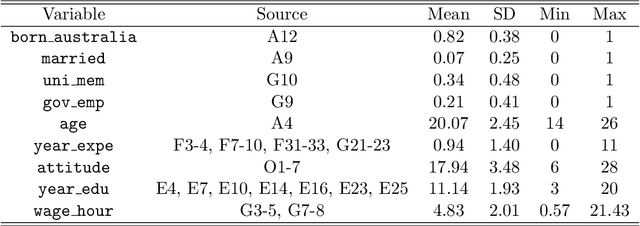
Recently, there has been a surge in methodological development for the difference-in-differences (DiD) approach to evaluate causal effects. Standard methods in the literature rely on the parallel trends assumption to identify the average treatment effect on the treated. However, the parallel trends assumption may be violated in the presence of unmeasured confounding, and the average treatment effect on the treated may not be useful in learning a treatment assignment policy for the entire population. In this article, we propose a general instrumented DiD approach for learning the optimal treatment policy. Specifically, we establish identification results using a binary instrumental variable (IV) when the parallel trends assumption fails to hold. Additionally, we construct a Wald estimator, novel inverse probability weighting (IPW) estimators, and a class of semiparametric efficient and multiply robust estimators, with theoretical guarantees on consistency and asymptotic normality, even when relying on flexible machine learning algorithms for nuisance parameters estimation. Furthermore, we extend the instrumented DiD to the panel data setting. We evaluate our methods in extensive simulations and a real data application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge