A Self-Encoder for Learning Nearest Neighbors
Paper and Code
Jun 25, 2023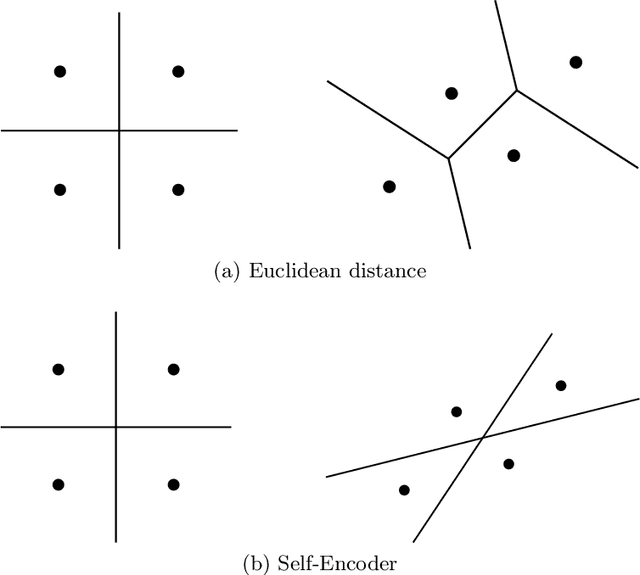
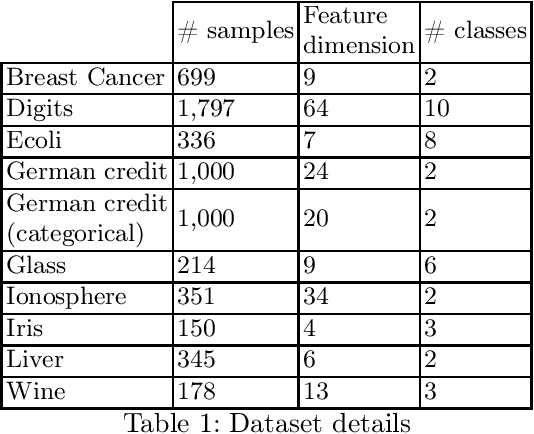
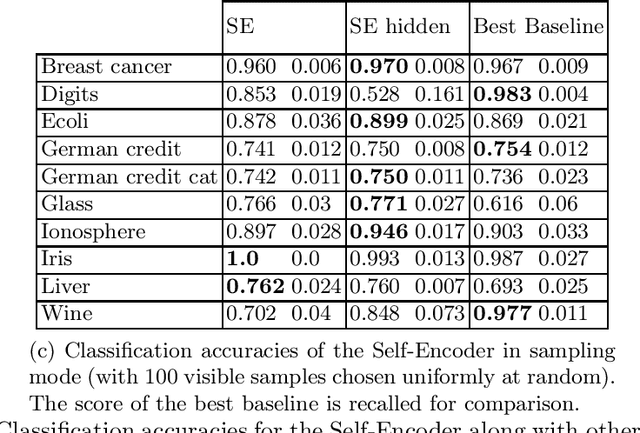
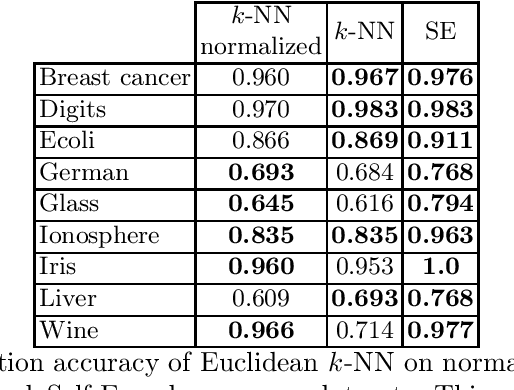
We present the self-encoder, a neural network trained to guess the identity of each data sample. Despite its simplicity, it learns a very useful representation of data, in a self-supervised way. Specifically, the self-encoder learns to distribute the data samples in the embedding space so that they are linearly separable from one another. This induces a geometry where two samples are close in the embedding space when they are not easy to differentiate. The self-encoder can then be combined with a nearest-neighbor classifier or regressor for any subsequent supervised task. Unlike regular nearest neighbors, the predictions resulting from this encoding of data are invariant to any scaling of features, making any preprocessing like min-max scaling not necessary. The experiments show the efficiency of the approach, especially on heterogeneous data mixing numerical features and categorical features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge