A second order primal-dual method for nonsmooth convex composite optimization
Paper and Code
Sep 05, 2017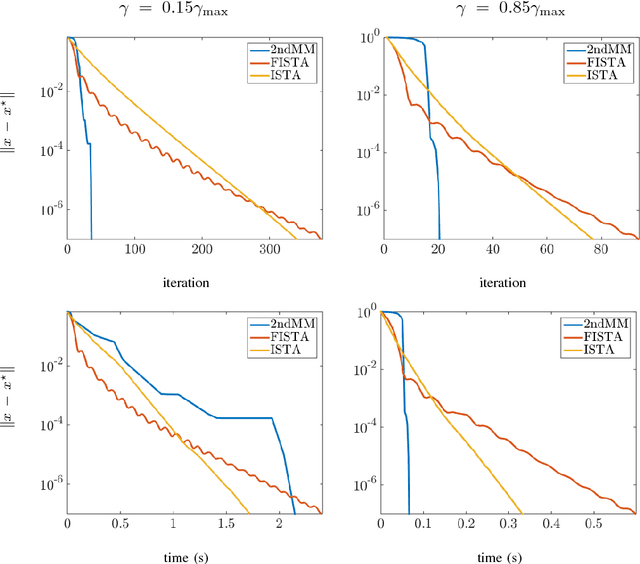
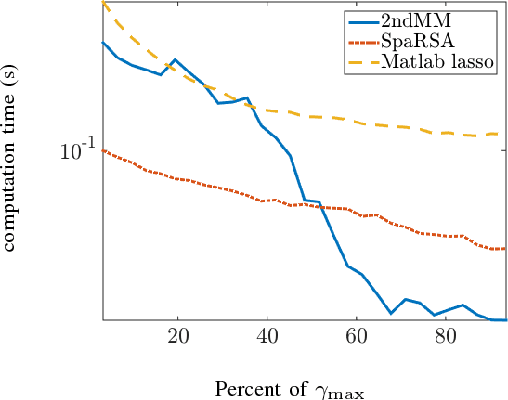
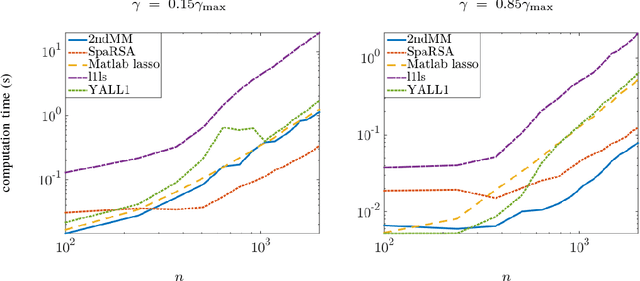
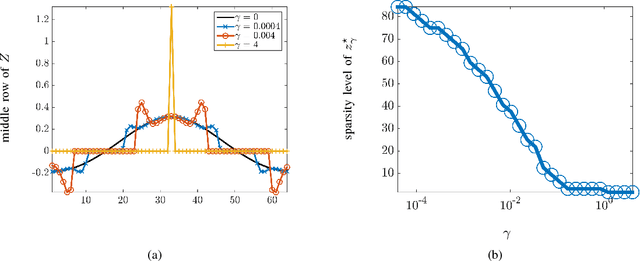
We develop a second order primal-dual method for optimization problems in which the objective function is given by the sum of a strongly convex twice differentiable term and a possibly nondifferentiable convex regularizer. After introducing an auxiliary variable, we utilize the proximal operator of the nonsmooth regularizer to transform the associated augmented Lagrangian into a function that is once, but not twice, continuously differentiable. The saddle point of this function corresponds to the solution of the original optimization problem. We employ a generalization of the Hessian to define second order updates on this function and prove global exponential stability of the corresponding differential inclusion. Furthermore, we develop a globally convergent customized algorithm that utilizes the primal-dual augmented Lagrangian as a merit function. We show that the search direction can be computed efficiently and prove quadratic/superlinear asymptotic convergence. We use the $\ell_1$-regularized least squares problem and the problem of designing a distributed controller for a spatially-invariant system to demonstrate the merits and the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge