A Real-Time Solver For Time-Optimal Control Of Omnidirectional Robots with Bounded Acceleration

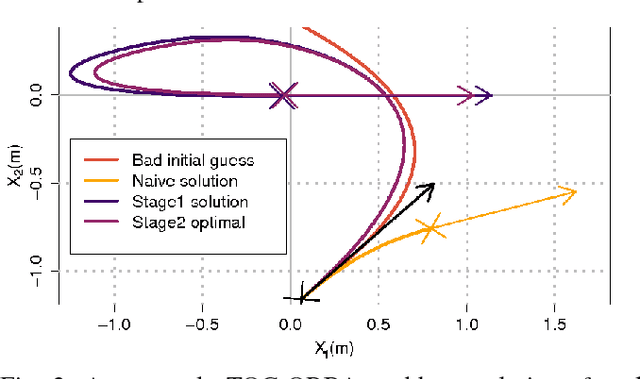
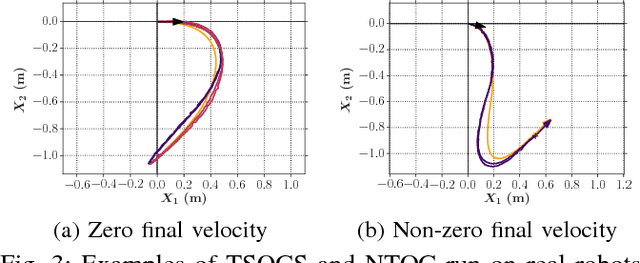
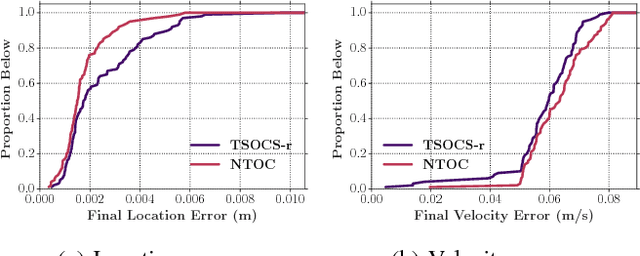
We are interested in the problem of time-optimal control of omnidirectional robots with bounded acceleration (TOC-ORBA). While there exist approximate solutions for such robots, and exact solutions with unbounded acceleration, exact solvers to the TOC-ORBA problem have remained elusive until now. In this paper, we present a real-time solver for true time-optimal control of omnidirectional robots with bounded acceleration. We first derive the general parameterized form of the solution to the TOC-ORBA problem by application of Pontryagin's maximum principle. We then frame the boundary value problem of TOC-ORBA as an optimization problem over the parametrized control space. To overcome local minima and poor initial guesses to the optimization problem, we introduce a two-stage optimal control solver (TSOCS): The first stage computes an upper bound to the total time for the TOC-ORBA problem and holds the time constant while optimizing the parameters of the trajectory to approach the boundary value conditions. The second stage uses the parameters found by the first stage, and relaxes the constraint on the total time to solve for the parameters of the complete TOC-ORBA problem. We further implement TSOCS as a closed loop controller to overcome actuation errors on real robots in real-time. We empirically demonstrate the effectiveness of TSOCS in simulation and on real robots, showing that 1) it runs in real time, generating solutions in less than 0.5ms on average; 2) it generates faster trajectories compared to an approximate solver; and 3) it is able to solve TOC-ORBA problems with non-zero final velocities that were previously unsolvable in real-time.