A provable SVD-based algorithm for learning topics in dominant admixture corpus

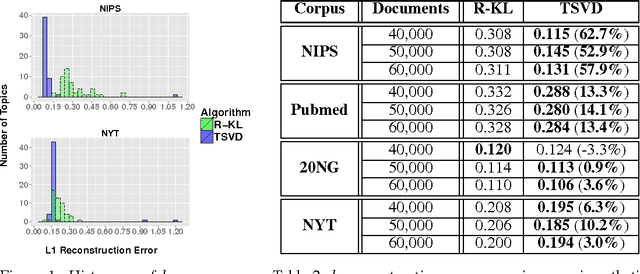
Topic models, such as Latent Dirichlet Allocation (LDA), posit that documents are drawn from admixtures of distributions over words, known as topics. The inference problem of recovering topics from admixtures, is NP-hard. Assuming separability, a strong assumption, [4] gave the first provable algorithm for inference. For LDA model, [6] gave a provable algorithm using tensor-methods. But [4,6] do not learn topic vectors with bounded $l_1$ error (a natural measure for probability vectors). Our aim is to develop a model which makes intuitive and empirically supported assumptions and to design an algorithm with natural, simple components such as SVD, which provably solves the inference problem for the model with bounded $l_1$ error. A topic in LDA and other models is essentially characterized by a group of co-occurring words. Motivated by this, we introduce topic specific Catchwords, group of words which occur with strictly greater frequency in a topic than any other topic individually and are required to have high frequency together rather than individually. A major contribution of the paper is to show that under this more realistic assumption, which is empirically verified on real corpora, a singular value decomposition (SVD) based algorithm with a crucial pre-processing step of thresholding, can provably recover the topics from a collection of documents drawn from Dominant admixtures. Dominant admixtures are convex combination of distributions in which one distribution has a significantly higher contribution than others. Apart from the simplicity of the algorithm, the sample complexity has near optimal dependence on $w_0$, the lowest probability that a topic is dominant, and is better than [4]. Empirical evidence shows that on several real world corpora, both Catchwords and Dominant admixture assumptions hold and the proposed algorithm substantially outperforms the state of the art [5].