A Probabilistic Framework for Discriminative and Neuro-Symbolic Semi-Supervised Learning
Paper and Code
Jun 10, 2020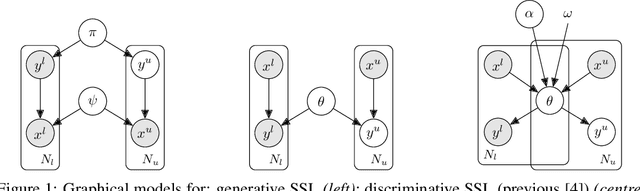

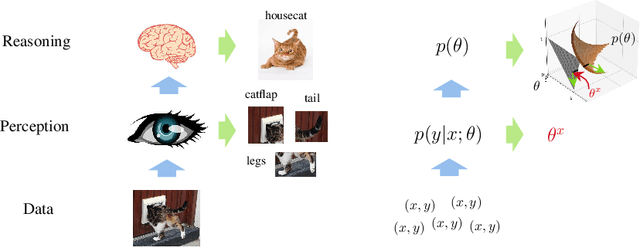
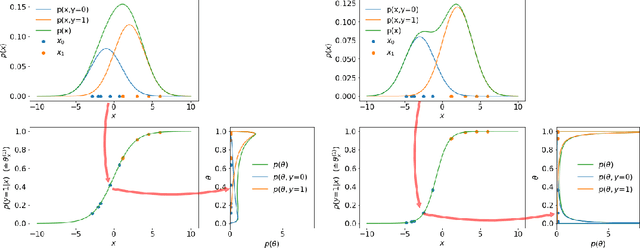
In semi-supervised learning (SSL), a rule to predict labels $y$ for data $x$ is learned from labelled data $(x^l,y^l)$ and unlabelled samples $x^u$. Strong progress has been made by combining a variety of methods, some of which pertain to $p(x)$, e.g. data augmentation that generates artificial samples from true $x$; whilst others relate to model outputs $p(y|x)$, e.g. regularising predictions on unlabelled data to minimise entropy or induce mutual exclusivity. Focusing on the latter, we fill a gap in the standard text by introducing a unifying probabilistic model for discriminative semi-supervised learning, mirroring that for classical generative methods. We show that several SSL methods can be theoretically justified under our model as inducing approximate priors over predicted parameters of $p(y|x)$. For tasks where labels represent binary attributes, our model leads to a principled approach to neuro-symbolic SSL, bridging the divide between statistical learning and logical rules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge