A Practical Index Structure Supporting Fréchet Proximity Queries Among Trajectories
Paper and Code
May 28, 2020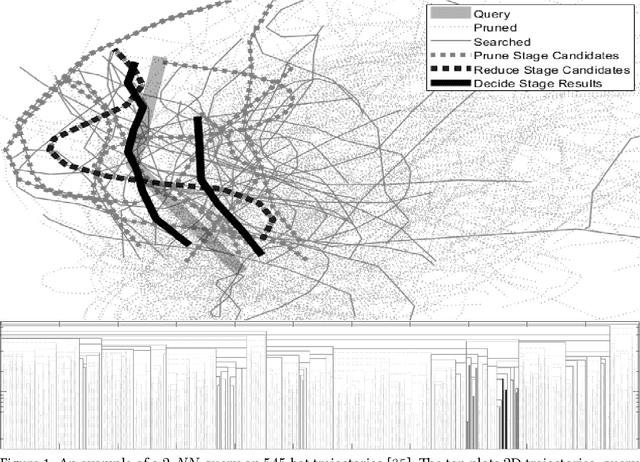

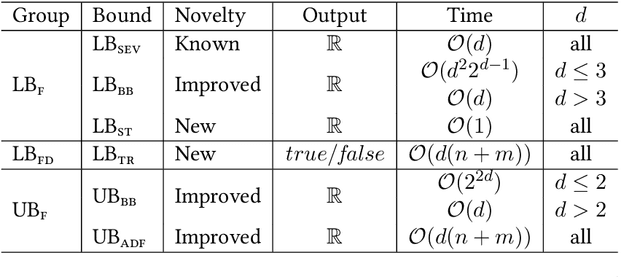
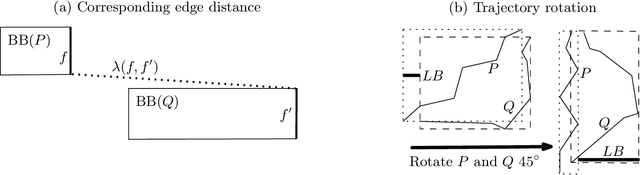
We present a scalable approach for range and $k$ nearest neighbor queries under computationally expensive metrics, like the continuous Fr\'echet distance on trajectory data. Based on clustering for metric indexes, we obtain a dynamic tree structure whose size is linear in the number of trajectories, regardless of the trajectory's individual sizes or the spatial dimension, which allows one to exploit low `intrinsic dimensionality' of data sets for effective search space pruning. Since the distance computation is expensive, generic metric indexing methods are rendered impractical. We present strategies that (i) improve on known upper and lower bound computations, (ii) build cluster trees without any or very few distance calls, and (iii) search using bounds for metric pruning, interval orderings for reduction, and randomized pivoting for reporting the final results. We analyze the efficiency and effectiveness of our methods with extensive experiments on diverse synthetic and real-world data sets. The results show improvement over state-of-the-art methods for exact queries, and even further speed-ups are achieved for queries that may return approximate results. Surprisingly, the majority of exact nearest-neighbor queries on real data sets are answered without any distance computations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge