A persistent homology approach to heart rate variability analysis with an application to sleep-wake classification

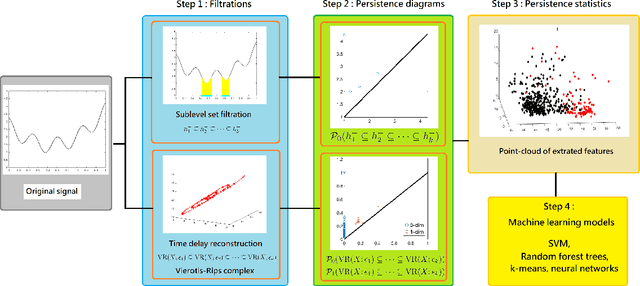
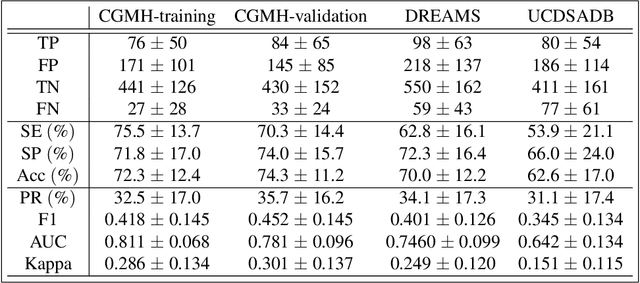
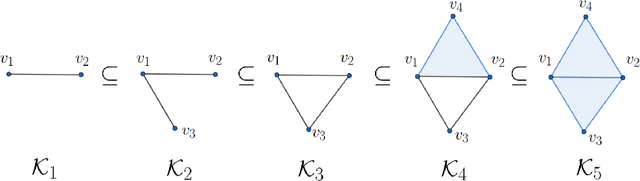
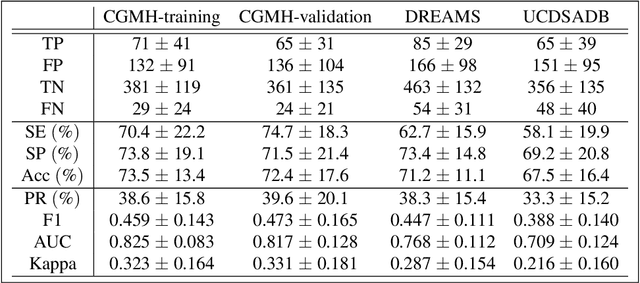
Persistent homology (PH) is a recently developed theory in the field of algebraic topology. It is an effective and robust tool to study shapes of datasets and has been widely applied. We demonstrate a general pipeline to apply PH to study time series; particularly the heart rate variability (HRV). First, we study the shapes of time series in two different ways -- sub-level set and Taken's lag map. Second, we propose a systematic approach to summarize/vectorize persistence diagrams, a companion tool of PH. To demonstrate our proposed method, we apply these tools to the HRV analysis and the sleep-wake, REM-NREM (rapid eyeball movement and non rapid eyeball movement) and sleep-REM-NREM classification problems. The proposed algorithm is evaluated on three different datasets via the cross-database validation scheme. The performance of our approach is comparable with the state-of-the-art algorithms, and are consistent throughout these different datasets.