A Penalty Approach for Normalizing Feature Distributions to Build Confounder-Free Models
Paper and Code
Jul 11, 2022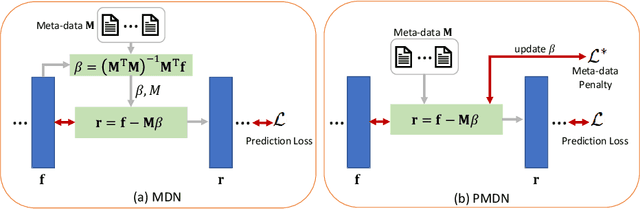

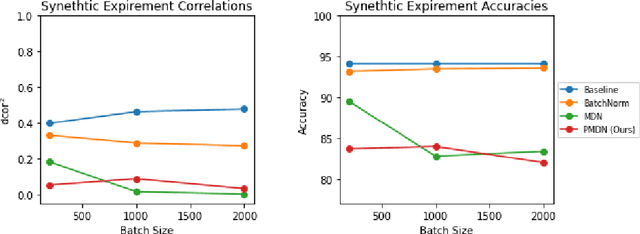
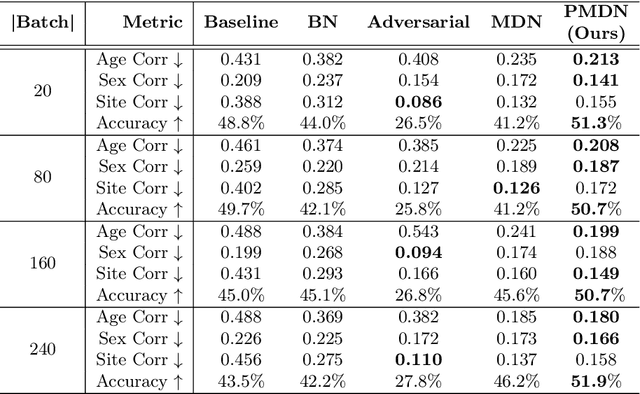
Translating machine learning algorithms into clinical applications requires addressing challenges related to interpretability, such as accounting for the effect of confounding variables (or metadata). Confounding variables affect the relationship between input training data and target outputs. When we train a model on such data, confounding variables will bias the distribution of the learned features. A recent promising solution, MetaData Normalization (MDN), estimates the linear relationship between the metadata and each feature based on a non-trainable closed-form solution. However, this estimation is confined by the sample size of a mini-batch and thereby may cause the approach to be unstable during training. In this paper, we extend the MDN method by applying a Penalty approach (referred to as PDMN). We cast the problem into a bi-level nested optimization problem. We then approximate this optimization problem using a penalty method so that the linear parameters within the MDN layer are trainable and learned on all samples. This enables PMDN to be plugged into any architectures, even those unfit to run batch-level operations, such as transformers and recurrent models. We show improvement in model accuracy and greater independence from confounders using PMDN over MDN in a synthetic experiment and a multi-label, multi-site dataset of magnetic resonance images (MRIs).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge