A novel Deep Learning approach for one-step Conformal Prediction approximation
Paper and Code
Jul 29, 2022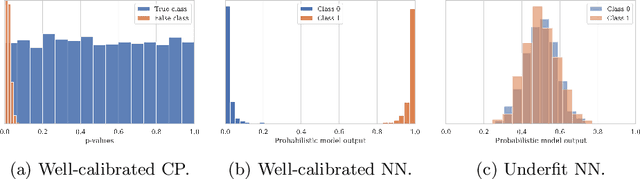


Deep Learning predictions with measurable confidence are increasingly desirable for real-world problems, especially in high-risk settings. The Conformal Prediction (CP) framework is a versatile solution that automatically guarantees a maximum error rate. However, CP suffers from computational inefficiencies that limit its application to large-scale datasets. In this paper, we propose a novel conformal loss function that approximates the traditionally two-step CP approach in a single step. By evaluating and penalising deviations from the stringent expected CP output distribution, a Deep Learning model may learn the direct relationship between input data and conformal p-values. Our approach achieves significant training time reductions up to 86% compared to Aggregated Conformal Prediction (ACP), an accepted CP approximation variant. In terms of approximate validity and predictive efficiency, we carry out a comprehensive empirical evaluation to show our novel loss function's competitiveness with ACP for binary and multi-class classification on the well-established MNIST dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge