A novel adaptive learning rate scheduler for deep neural networks

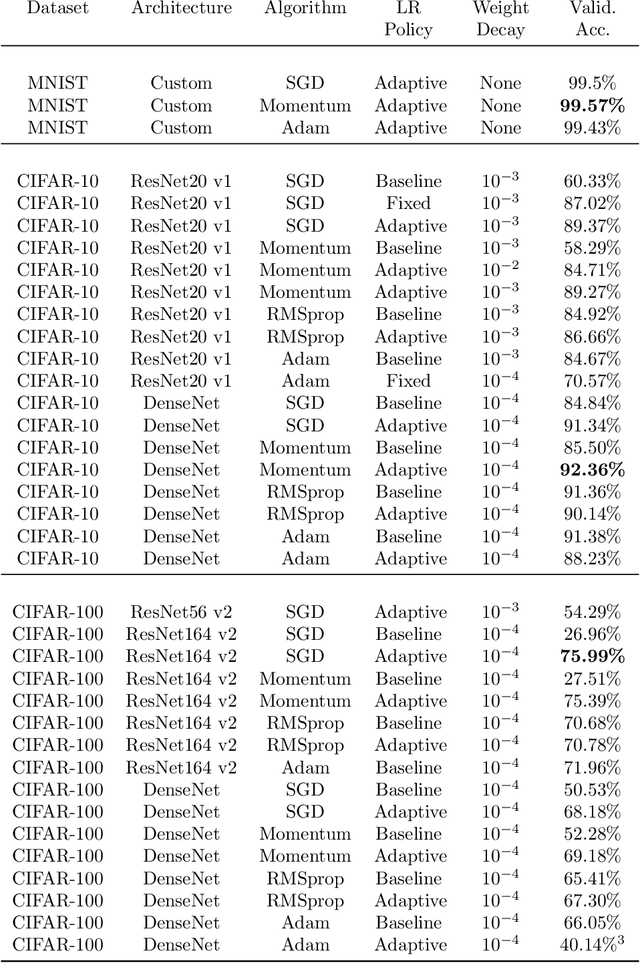
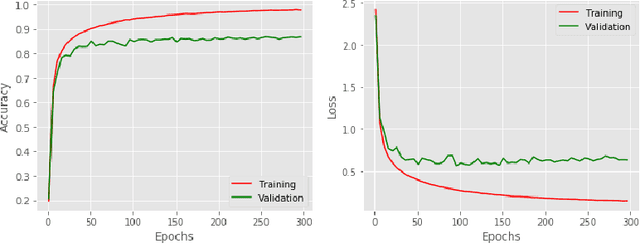
Optimizing deep neural networks is largely thought to be an empirical process, requiring manual tuning of several hyper-parameters, such as learning rate, weight decay, and dropout rate. Arguably, the learning rate is the most important of these to tune, and this has gained more attention in recent works. In this paper, we propose a novel method to compute the learning rate for training deep neural networks with stochastic gradient descent. We first derive a theoretical framework to compute learning rates dynamically based on the Lipschitz constant of the loss function. We then extend this framework to other commonly used optimization algorithms, such as gradient descent with momentum and Adam. We run an extensive set of experiments that demonstrate the efficacy of our approach on popular architectures and datasets, and show that commonly used learning rates are an order of magnitude smaller than the ideal value.