A Novel Adaptive Causal Sampling Method for Physics-Informed Neural Networks
Paper and Code
Oct 24, 2022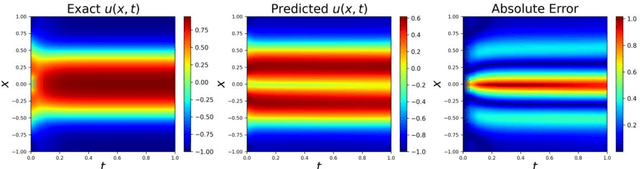
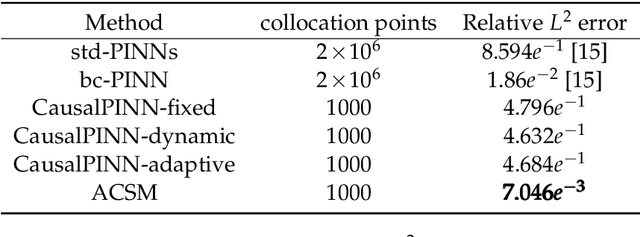
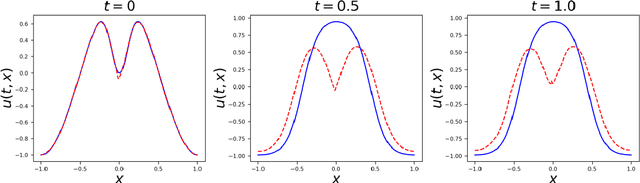
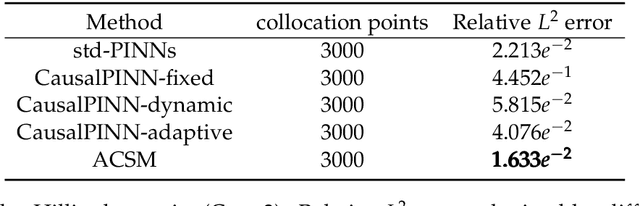
Physics-Informed Neural Networks (PINNs) have become a kind of attractive machine learning method for obtaining solutions of partial differential equations (PDEs). Training PINNs can be seen as a semi-supervised learning task, in which only exact values of initial and boundary points can be obtained in solving forward problems, and in the whole spatio-temporal domain collocation points are sampled without exact labels, which brings training difficulties. Thus the selection of collocation points and sampling methods are quite crucial in training PINNs. Existing sampling methods include fixed and dynamic types, and in the more popular latter one, sampling is usually controlled by PDE residual loss. We point out that it is not sufficient to only consider the residual loss in adaptive sampling and sampling should obey temporal causality. We further introduce temporal causality into adaptive sampling and propose a novel adaptive causal sampling method to improve the performance and efficiency of PINNs. Numerical experiments of several PDEs with high-order derivatives and strong nonlinearity, including Cahn Hilliard and KdV equations, show that the proposed sampling method can improve the performance of PINNs with few collocation points. We demonstrate that by utilizing such a relatively simple sampling method, prediction performance can be improved up to two orders of magnitude compared with state-of-the-art results with almost no extra computation cost, especially when points are limited.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge