A Non-Parametric Control Chart For High Frequency Multivariate Data
Paper and Code
Jul 29, 2016

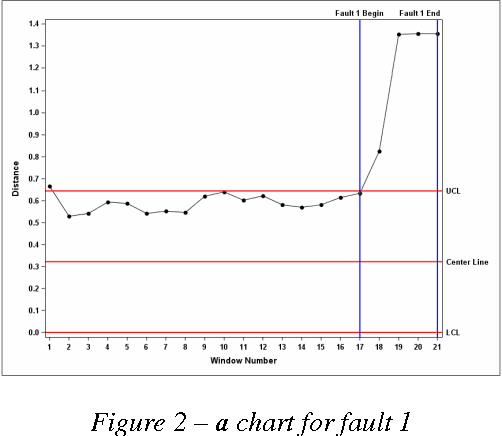
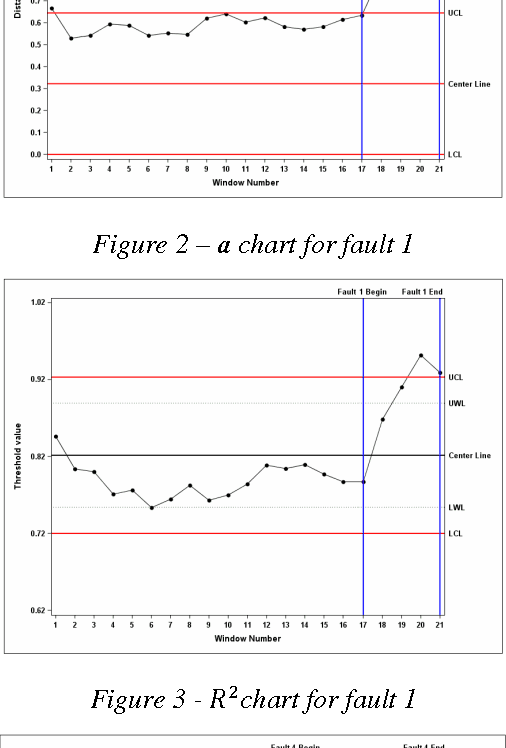
Support Vector Data Description (SVDD) is a machine learning technique used for single class classification and outlier detection. SVDD based K-chart was first introduced by Sun and Tsung for monitoring multivariate processes when underlying distribution of process parameters or quality characteristics depart from Normality. The method first trains a SVDD model on data obtained from stable or in-control operations of the process to obtain a threshold $R^2$ and kernel center a. For each new observation, its Kernel distance from the Kernel center a is calculated. The kernel distance is compared against the threshold $R^2$ to determine if the observation is within the control limits. The non-parametric K-chart provides an attractive alternative to the traditional control charts such as the Hotelling's $T^2$ charts when distribution of the underlying multivariate data is either non-normal or is unknown. But there are challenges when K-chart is deployed in practice. The K-chart requires calculating kernel distance of each new observation but there are no guidelines on how to interpret the kernel distance plot and infer about shifts in process mean or changes in process variation. This limits the application of K-charts in big-data applications such as equipment health monitoring, where observations are generated at a very high frequency. In this scenario, the analyst using the K-chart is inundated with kernel distance results at a very high frequency, generally without any recourse for detecting presence of any assignable causes of variation. We propose a new SVDD based control chart, called as $K_T$ chart, which addresses challenges encountered when using K-chart for big-data applications. The $K_T$ charts can be used to simultaneously track process variation and central tendency. We illustrate the successful use of $K_T$ chart using the Tennessee Eastman process data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge