A New Random Reshuffling Method for Nonsmooth Nonconvex Finite-sum Optimization

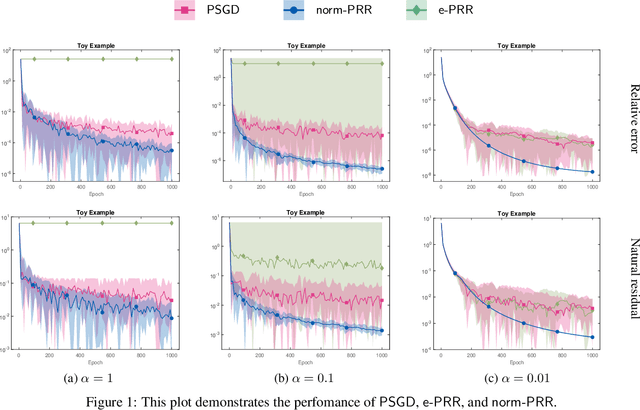
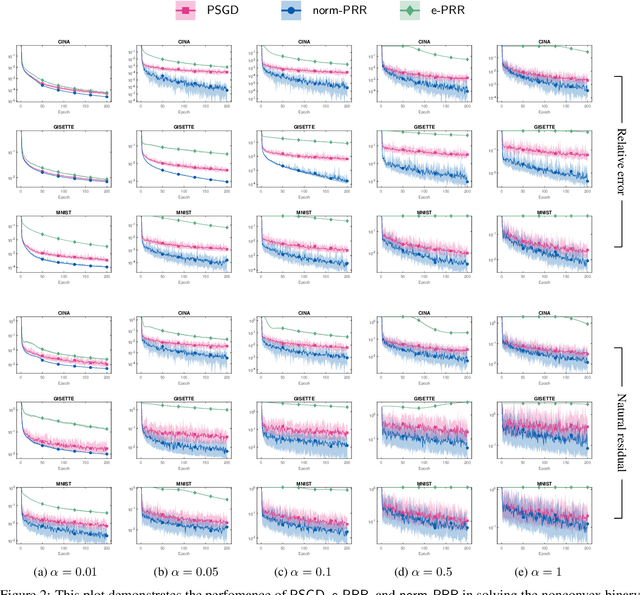
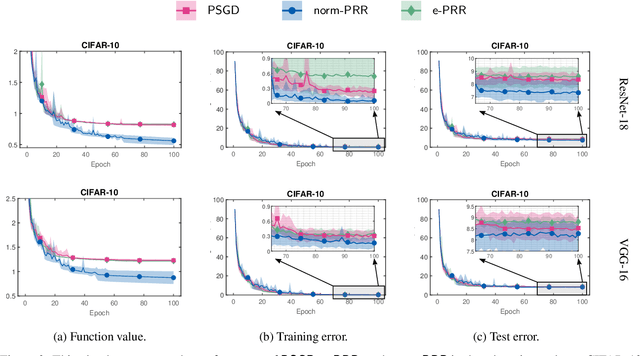
In this work, we propose and study a novel stochastic optimization algorithm, termed the normal map-based proximal random reshuffling (norm-PRR) method, for nonsmooth nonconvex finite-sum problems. Random reshuffling techniques are prevalent and widely utilized in large-scale applications, e.g., in the training of neural networks. While the convergence behavior and advantageous acceleration effects of random reshuffling methods are fairly well understood in the smooth setting, much less seems to be known in the nonsmooth case and only few proximal-type random reshuffling approaches with provable guarantees exist. We establish the iteration complexity ${\cal O}(n^{-1/3}T^{-2/3})$ for norm-PRR, where $n$ is the number of component functions and $T$ counts the total number of iteration. We also provide novel asymptotic convergence results for norm-PRR. Specifically, under the Kurdyka-{\L}ojasiewicz (KL) inequality, we establish strong limit-point convergence, i.e., the iterates generated by norm-PRR converge to a single stationary point. Moreover, we derive last iterate convergence rates of the form ${\cal O}(k^{-p})$; here, $p \in [0, 1]$ depends on the KL exponent $\theta \in [0,1)$ and step size dynamics. Finally, we present preliminary numerical results on machine learning problems that demonstrate the efficiency of the proposed method.