A New Neural Network Architecture Invariant to the Action of Symmetry Subgroups
Paper and Code
Dec 11, 2020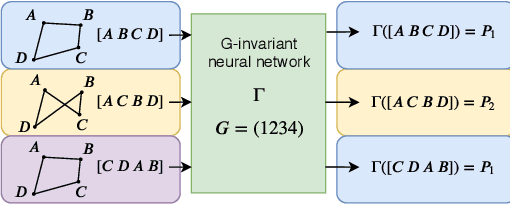

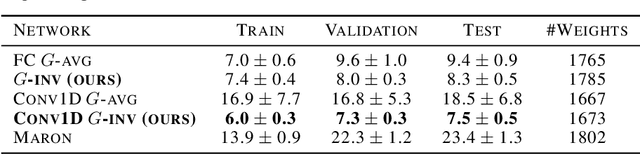
We propose a computationally efficient $G$-invariant neural network that approximates functions invariant to the action of a given permutation subgroup $G \leq S_n$ of the symmetric group on input data. The key element of the proposed network architecture is a new $G$-invariant transformation module, which produces a $G$-invariant latent representation of the input data. Theoretical considerations are supported by numerical experiments, which demonstrate the effectiveness and strong generalization properties of the proposed method in comparison to other $G$-invariant neural networks.
* Presented as contributed talk at NeurIPS 2020 workshop on
Differential Geometry meets Deep Learning
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge