A new distance measurement and its application in K-Means Algorithm
Paper and Code
Jun 10, 2022
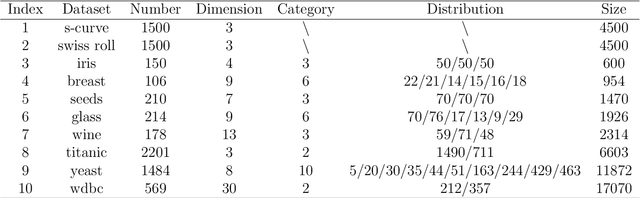

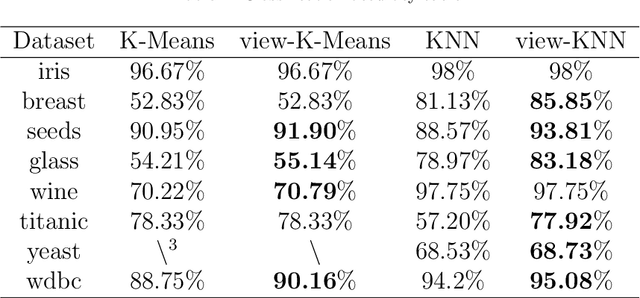
K-Means clustering algorithm is one of the most commonly used clustering algorithms because of its simplicity and efficiency. K-Means clustering algorithm based on Euclidean distance only pays attention to the linear distance between samples, but ignores the overall distribution structure of the dataset (i.e. the fluid structure of dataset). Since it is difficult to describe the internal structure of two data points by Euclidean distance in high-dimensional data space, we propose a new distance measurement, namely, view-distance, and apply it to the K-Means algorithm. On the classical manifold learning datasets, S-curve and Swiss roll datasets, not only this new distance can cluster the data according to the structure of the data itself, but also the boundaries between categories are neat dividing lines. Moreover, we also tested the classification accuracy and clustering effect of the K-Means algorithm based on view-distance on some real-world datasets. The experimental results show that, on most datasets, the K-Means algorithm based on view-distance has a certain degree of improvement in classification accuracy and clustering effect.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge