A New Correction to the Rytov Approximation for Strongly Scattering Lossy Media

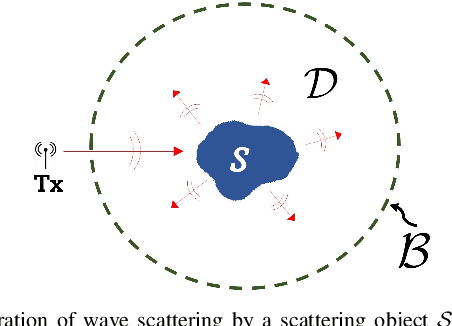
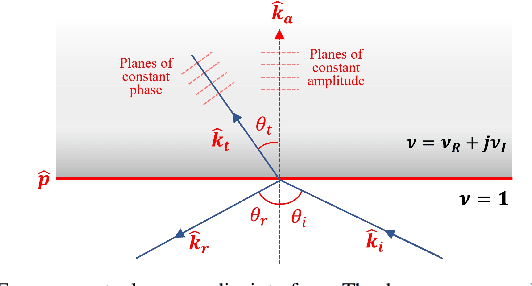
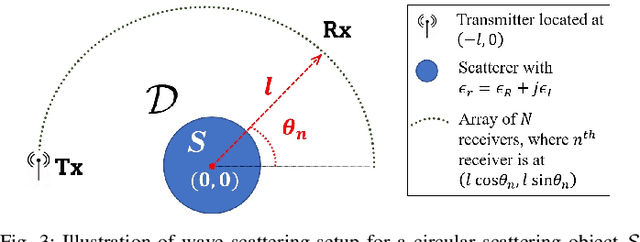
We propose a correction to the conventional Rytov approximation (RA) and investigate its performance for predicting wave scattering under strong scattering conditions. An important motivation for the correction and investigation is to help in the development of better models for inverse scattering. The correction is based upon incorporating the high frequency theory of inhomogeneous wave propagation for lossy media into the RA formulation. We denote the technique as the extended Rytov approximation for lossy media (xRA-LM). xRA-LM significantly improves upon existing non-iterative linear scattering approximations such as RA and the Born approximation (BA) by providing a validity range for the permittivity of the objects of up to 50 times greater than RA. We demonstrate the technique by providing results for predicting wave scattering from piece-wise homogeneous scatterers in a two-dimensional (2D) region. Numerical investigation of the performance of xRA-LM for solving direct problem show that xRA-LM can accurately predict wave scattering by electrically large, low-loss scatterers with high complex permittivity ($\epsilon_r> 50+5j$). To the best of our knowledge, this is the first non-iterative, linear approximate wave scattering model which has a large validity range in terms of both permittivity and electrical size.