A New Basis for Sparse PCA

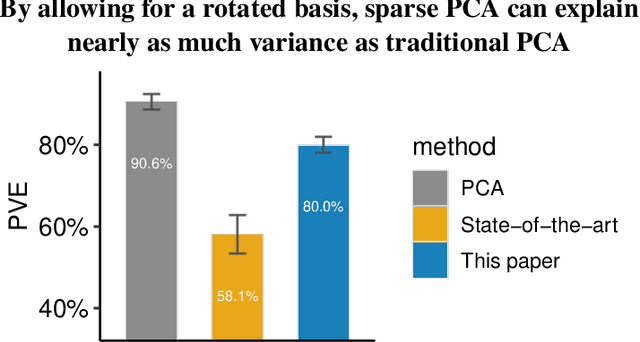
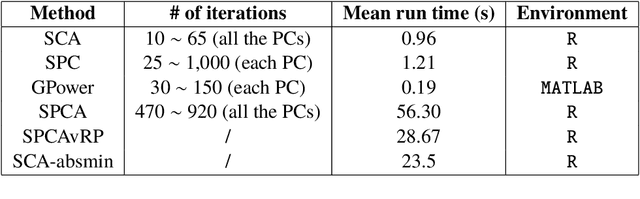
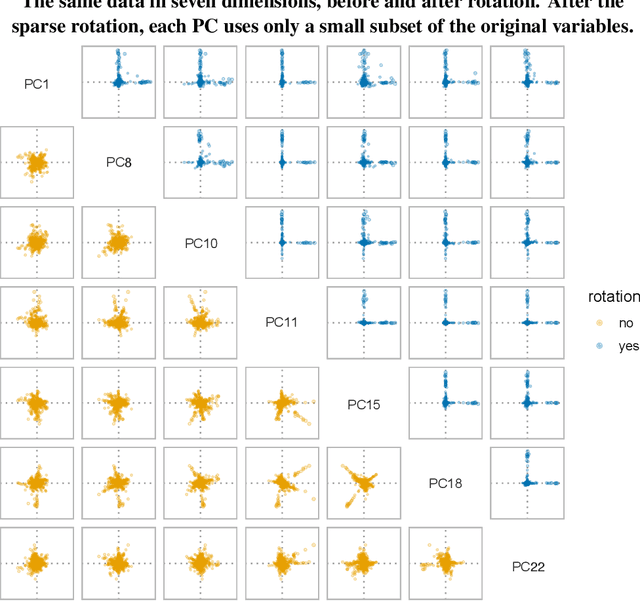
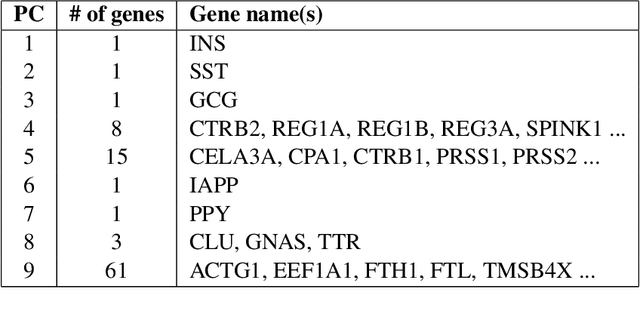
The statistical and computational performance of sparse principal component analysis (PCA) can be dramatically improved when the principal components are allowed to be sparse in a rotated eigenbasis. For this, we propose a new method for sparse PCA. In the simplest version of the algorithm, the component scores and loadings are initialized with a low-rank singular value decomposition. Then, the singular vectors are rotated with orthogonal rotations to make them approximately sparse. Finally, soft-thresholding is applied to the rotated singular vectors. This approach differs from prior approaches because it uses an orthogonal rotation to approximate a sparse basis. Our sparse PCA framework is versatile; for example, it extends naturally to the two-way analysis of a data matrix for simultaneous dimensionality reduction of rows and columns. We identify the close relationship between sparse PCA and independent component analysis for separating sparse signals. We provide empirical evidence showing that for the same level of sparsity, the proposed sparse PCA method is more stable and can explain more variance compared to alternative methods. Through three applications---sparse coding of images, analysis of transcriptome sequencing data, and large-scale clustering of Twitter accounts, we demonstrate the usefulness of sparse PCA in exploring modern multivariate data.