A Natural Actor-Critic Algorithm with Downside Risk Constraints
Paper and Code
Jul 08, 2020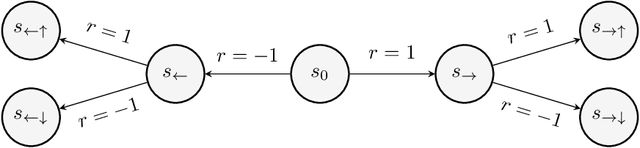
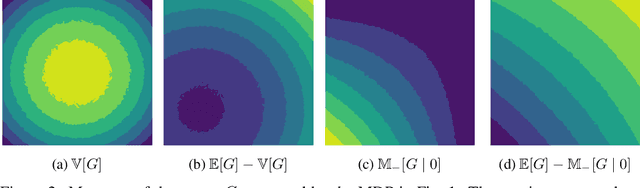
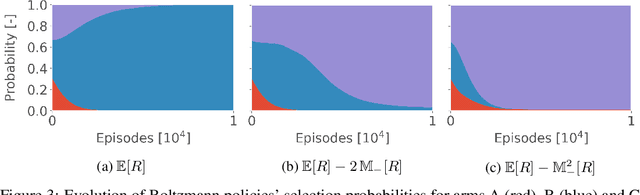
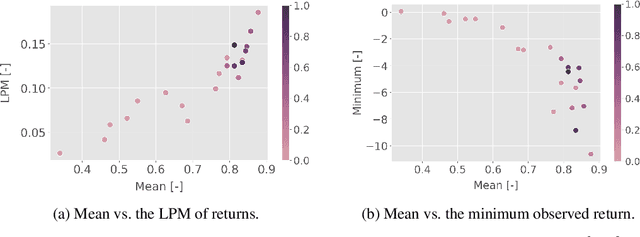
Existing work on risk-sensitive reinforcement learning - both for symmetric and downside risk measures - has typically used direct Monte-Carlo estimation of policy gradients. While this approach yields unbiased gradient estimates, it also suffers from high variance and decreased sample efficiency compared to temporal-difference methods. In this paper, we study prediction and control with aversion to downside risk which we gauge by the lower partial moment of the return. We introduce a new Bellman equation that upper bounds the lower partial moment, circumventing its non-linearity. We prove that this proxy for the lower partial moment is a contraction, and provide intuition into the stability of the algorithm by variance decomposition. This allows sample-efficient, on-line estimation of partial moments. For risk-sensitive control, we instantiate Reward Constrained Policy Optimization, a recent actor-critic method for finding constrained policies, with our proxy for the lower partial moment. We extend the method to use natural policy gradients and demonstrate the effectiveness of our approach on three benchmark problems for risk-sensitive reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge