A method for estimating the entropy of time series using artificial neural network
Paper and Code
Jul 18, 2021
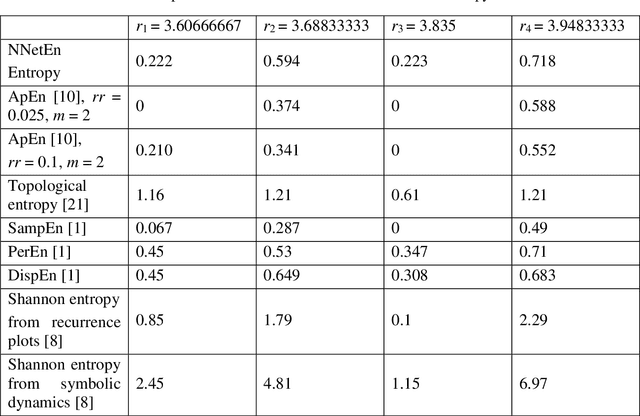

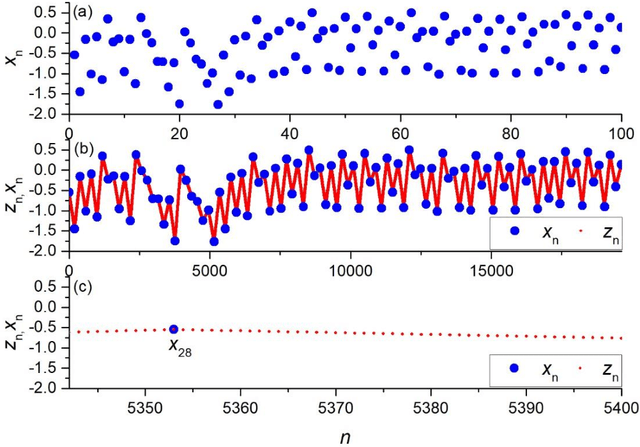
Measuring the predictability and complexity of time series is an essential tool in designing and controlling the nonlinear system. There exist different entropy measures in the literature to analyze the predictability and complexity of time series. However, these measures have some drawbacks especially in short time series. To overcome the difficulties, this paper proposes a new method for estimating the entropy of a time series using the LogNNet 784:25:10 neural network model. The LogNNet reservoir matrix consists of 19625 elements which is filled with the time series elements. After that, the network is trained on MNIST-10 dataset and the classification accuracy is calculated. The accuracy is considered as the entropy measure and denoted by NNetEn. A more complex transformation of the input information by the time series in the reservoir leads to higher NNetEn values. Many practical time series data have less than 19625 elements. Some duplicating or stretching methods are investigated to overcome this difficulty and the most successful method is identified for practical applications. The epochs number in the training process of LogNNet is considered as the input parameter. A new time series characteristic called time series learning inertia is introduced to investigate the effect of epochs number in the efficiency of neural network. To show the robustness and efficiency of the proposed method, it is applied on some chaotic, periodic, random, binary and constant time series. The NNetEn is compared with some existing entropy measures. The results show that the proposed method is more robust and accurate than existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge