A Message Passing Algorithm for the Problem of Path Packing in Graphs
Paper and Code
Mar 18, 2016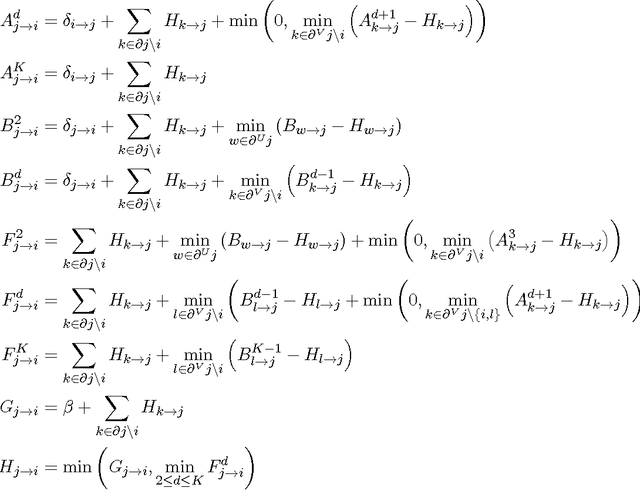
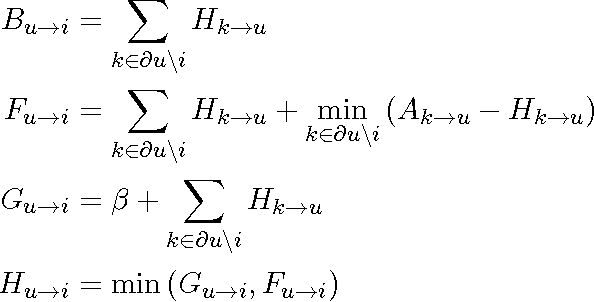
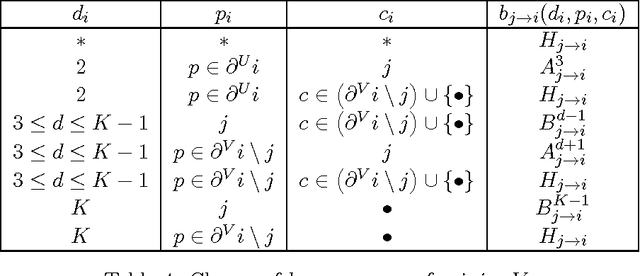
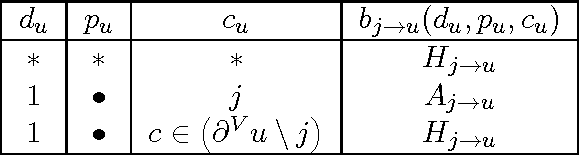
We consider the problem of packing node-disjoint directed paths in a directed graph. We consider a variant of this problem where each path starts within a fixed subset of root nodes, subject to a given bound on the length of paths. This problem is motivated by the so-called kidney exchange problem, but has potential other applications and is interesting in its own right. We propose a new algorithm for this problem based on the message passing/belief propagation technique. A priori this problem does not have an associated graphical model, so in order to apply a belief propagation algorithm we provide a novel representation of the problem as a graphical model. Standard belief propagation on this model has poor scaling behavior, so we provide an efficient implementation that significantly decreases the complexity. We provide numerical results comparing the performance of our algorithm on both artificially created graphs and real world networks to several alternative algorithms, including algorithms based on integer programming (IP) techniques. These comparisons show that our algorithm scales better to large instances than IP-based algorithms and often finds better solutions than a simple algorithm that greedily selects the longest path from each root node. In some cases it also finds better solutions than the ones found by IP-based algorithms even when the latter are allowed to run significantly longer than our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge