A Machine Learning Approach to Predicting the Smoothed Complexity of Sorting Algorithms

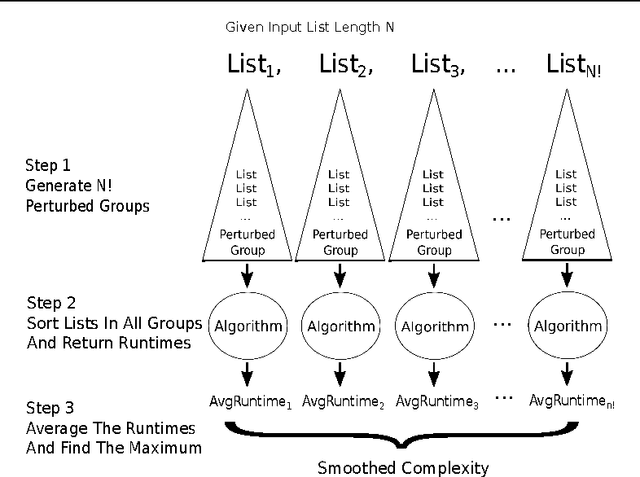
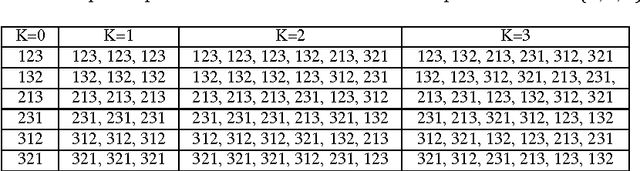
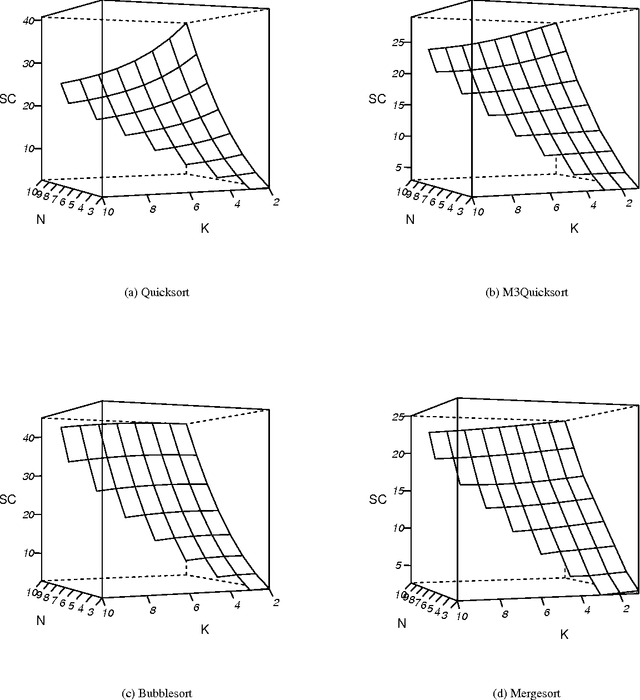
Smoothed analysis is a framework for analyzing the complexity of an algorithm, acting as a bridge between average and worst-case behaviour. For example, Quicksort and the Simplex algorithm are widely used in practical applications, despite their heavy worst-case complexity. Smoothed complexity aims to better characterize such algorithms. Existing theoretical bounds for the smoothed complexity of sorting algorithms are still quite weak. Furthermore, empirically computing the smoothed complexity via its original definition is computationally infeasible, even for modest input sizes. In this paper, we focus on accurately predicting the smoothed complexity of sorting algorithms, using machine learning techniques. We propose two regression models that take into account various properties of sorting algorithms and some of the known theoretical results in smoothed analysis to improve prediction quality. We show experimental results for predicting the smoothed complexity of Quicksort, Mergesort, and optimized Bubblesort for large input sizes, therefore filling the gap between known theoretical and empirical results.