A Linear-Time Particle Gibbs Sampler for Infinite Hidden Markov Models

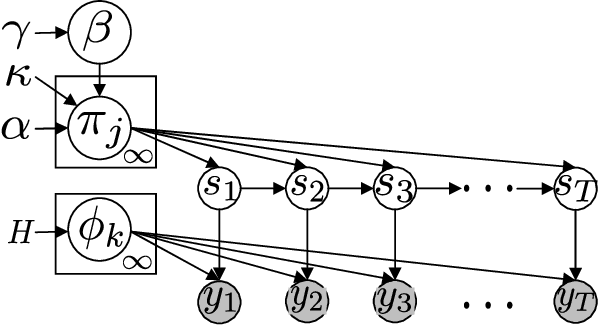
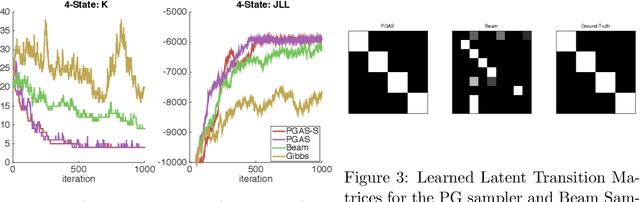
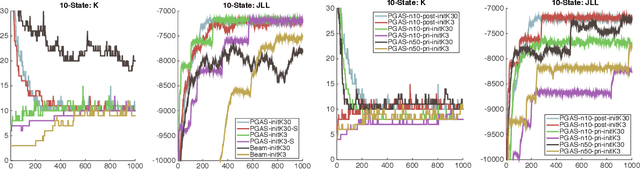
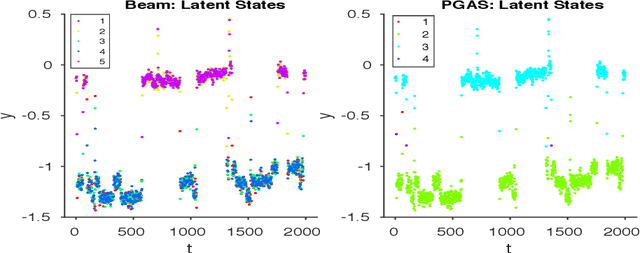
Infinite Hidden Markov Models (iHMM's) are an attractive, nonparametric generalization of the classical Hidden Markov Model which can automatically infer the number of hidden states in the system. However, due to the infinite-dimensional nature of transition dynamics performing inference in the iHMM is difficult. In this paper, we present an infinite-state Particle Gibbs (PG) algorithm to resample state trajectories for the iHMM. The proposed algorithm uses an efficient proposal optimized for iHMMs and leverages ancestor sampling to suppress degeneracy of the standard PG algorithm. Our algorithm demonstrates significant convergence improvements on synthetic and real world data sets. Additionally, the infinite-state PG algorithm has linear-time complexity in the number of states in the sampler, while competing methods scale quadratically.