A Linear-Programming Approximation of AC Power Flows
Paper and Code
Aug 06, 2013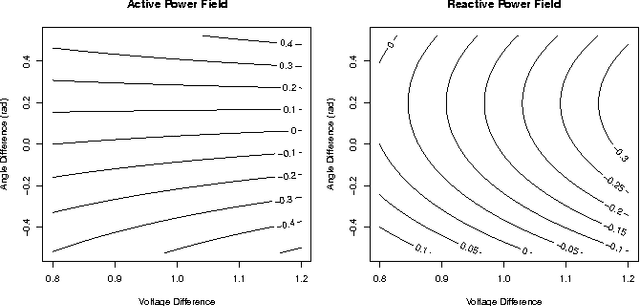
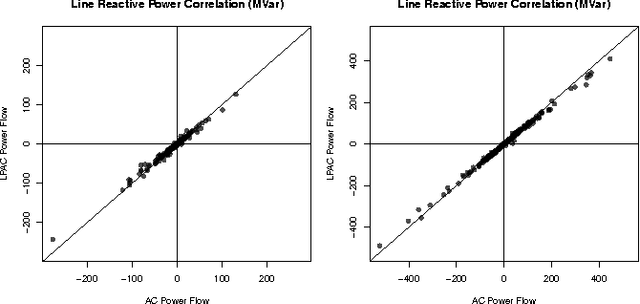
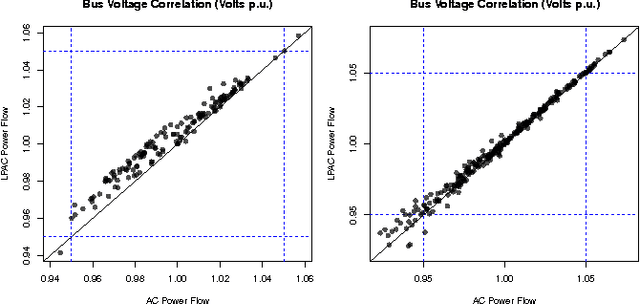
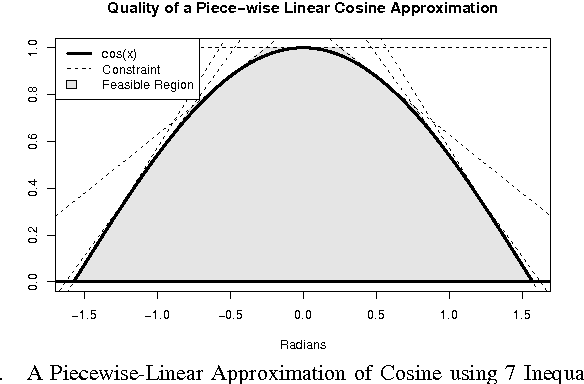
Linear active-power-only DC power flow approximations are pervasive in the planning and control of power systems. However, these approximations fail to capture reactive power and voltage magnitudes, both of which are necessary in many applications to ensure voltage stability and AC power flow feasibility. This paper proposes linear-programming models (the LPAC models) that incorporate reactive power and voltage magnitudes in a linear power flow approximation. The LPAC models are built on a convex approximation of the cosine terms in the AC equations, as well as Taylor approximations of the remaining nonlinear terms. Experimental comparisons with AC solutions on a variety of standard IEEE and MatPower benchmarks show that the LPAC models produce accurate values for active and reactive power, phase angles, and voltage magnitudes. The potential benefits of the LPAC models are illustrated on two "proof-of-concept" studies in power restoration and capacitor placement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge