A Linear Approximation to the chi^2 Kernel with Geometric Convergence

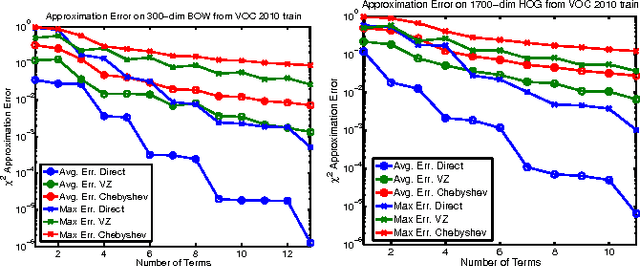
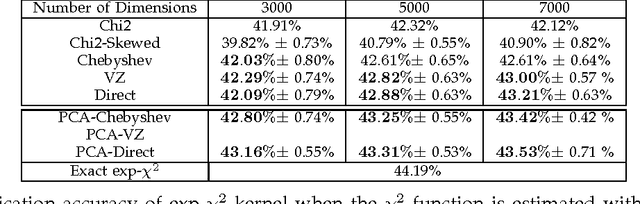
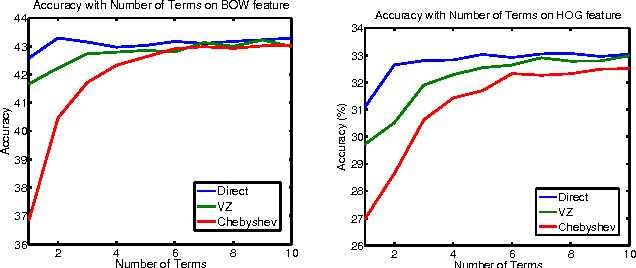
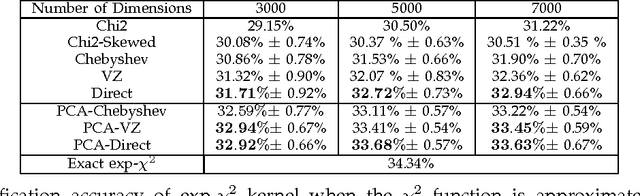
We propose a new analytical approximation to the $\chi^2$ kernel that converges geometrically. The analytical approximation is derived with elementary methods and adapts to the input distribution for optimal convergence rate. Experiments show the new approximation leads to improved performance in image classification and semantic segmentation tasks using a random Fourier feature approximation of the $\exp-\chi^2$ kernel. Besides, out-of-core principal component analysis (PCA) methods are introduced to reduce the dimensionality of the approximation and achieve better performance at the expense of only an additional constant factor to the time complexity. Moreover, when PCA is performed jointly on the training and unlabeled testing data, further performance improvements can be obtained. Experiments conducted on the PASCAL VOC 2010 segmentation and the ImageNet ILSVRC 2010 datasets show statistically significant improvements over alternative approximation methods.