A least squares support vector regression for anisotropic diffusion filtering
Paper and Code
Jan 30, 2022
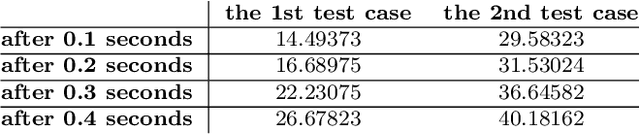


Anisotropic diffusion filtering for signal smoothing as a low-pass filter has the advantage of the edge-preserving, i.e., it does not affect the edges that contain more critical data than the other parts of the signal. In this paper, we present a numerical algorithm based on least squares support vector regression by using Legendre orthogonal kernel with the discretization of the nonlinear diffusion problem in time by the Crank-Nicolson method. This method transforms the signal smoothing process into solving an optimization problem that can be solved by efficient numerical algorithms. In the final analysis, we have reported some numerical experiments to show the effectiveness of the proposed machine learning based approach for signal smoothing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge