A Learning Theoretic Approach to Energy Harvesting Communication System Optimization
Paper and Code
Dec 06, 2012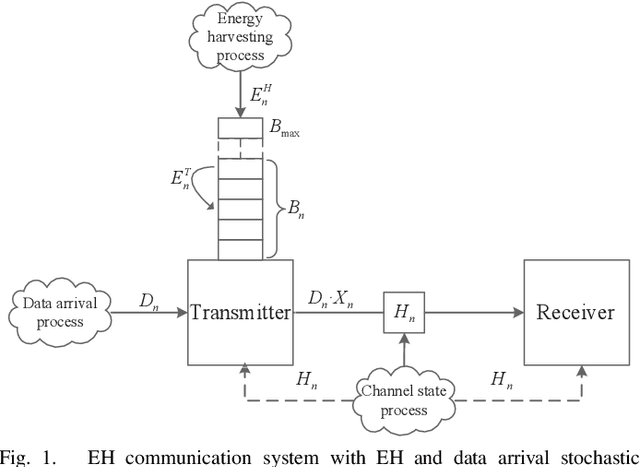
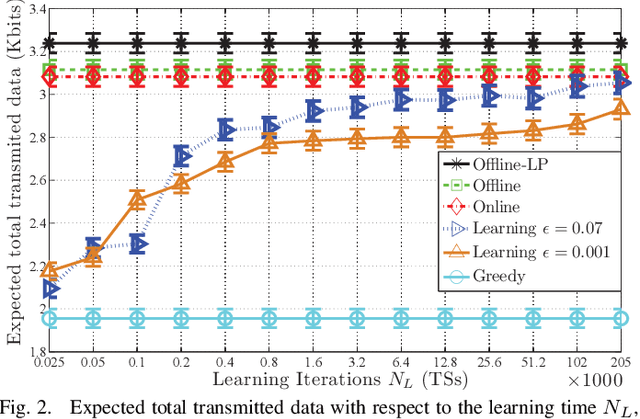
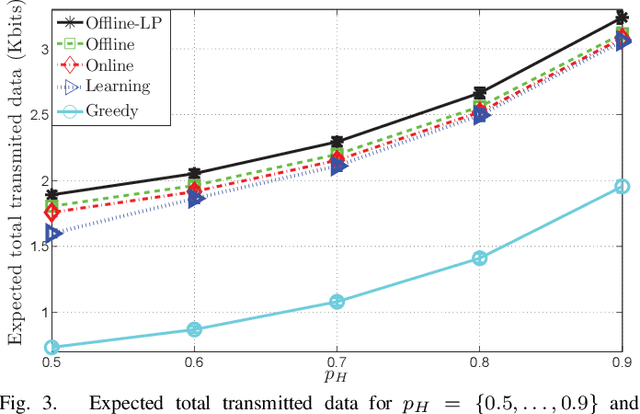
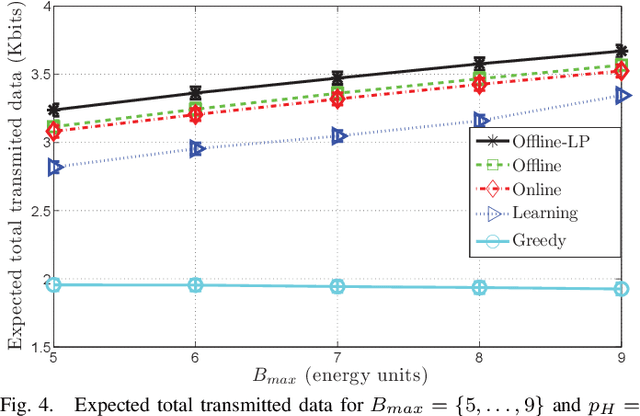
A point-to-point wireless communication system in which the transmitter is equipped with an energy harvesting device and a rechargeable battery, is studied. Both the energy and the data arrivals at the transmitter are modeled as Markov processes. Delay-limited communication is considered assuming that the underlying channel is block fading with memory, and the instantaneous channel state information is available at both the transmitter and the receiver. The expected total transmitted data during the transmitter's activation time is maximized under three different sets of assumptions regarding the information available at the transmitter about the underlying stochastic processes. A learning theoretic approach is introduced, which does not assume any a priori information on the Markov processes governing the communication system. In addition, online and offline optimization problems are studied for the same setting. Full statistical knowledge and causal information on the realizations of the underlying stochastic processes are assumed in the online optimization problem, while the offline optimization problem assumes non-causal knowledge of the realizations in advance. Comparing the optimal solutions in all three frameworks, the performance loss due to the lack of the transmitter's information regarding the behaviors of the underlying Markov processes is quantified.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge