A Layered Learning Approach to Scaling in Learning Classifier Systems for Boolean Problems
Paper and Code
Jun 02, 2020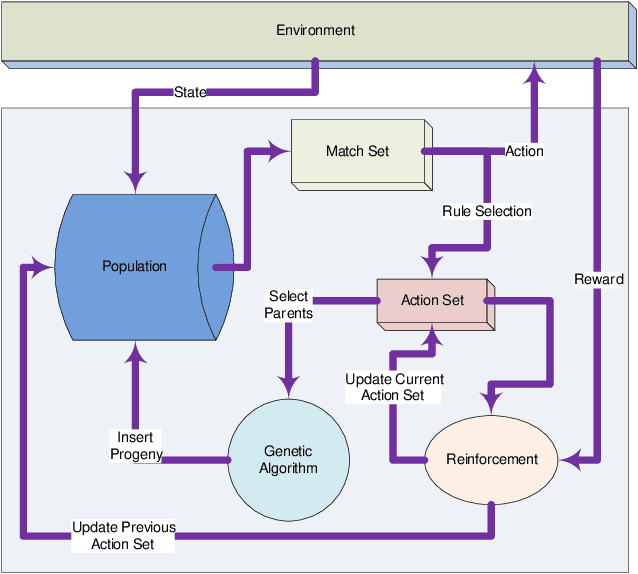
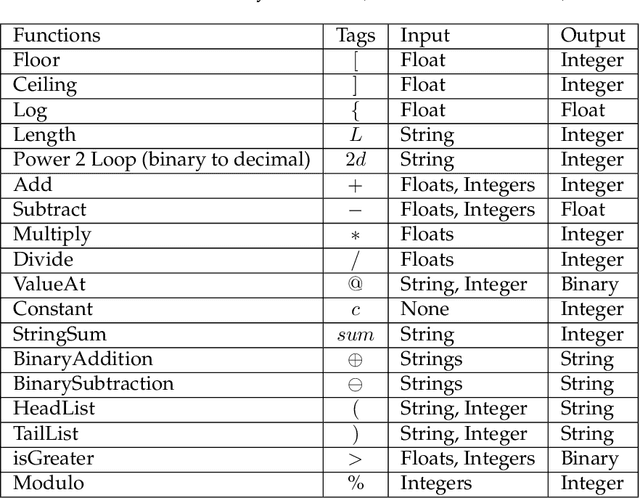
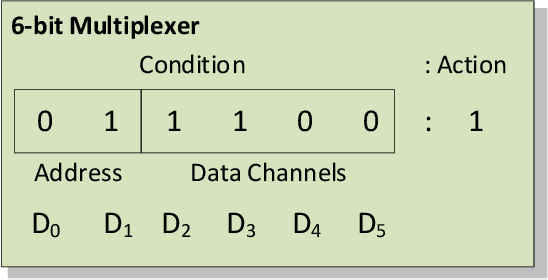
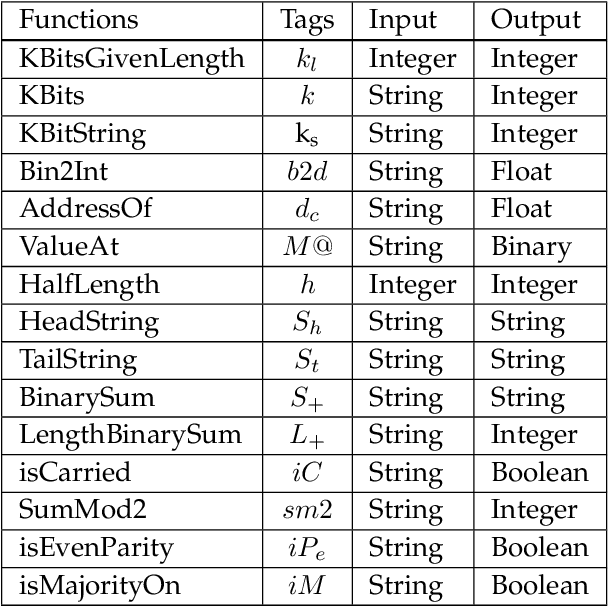
Learning classifier systems (LCSs) originated from cognitive-science research but migrated such that LCS became powerful classification techniques. Modern LCSs can be used to extract building blocks of knowledge to solve more difficult problems in the same or a related domain. Recent works on LCSs showed that the knowledge reuse through the adoption of Code Fragments, GP-like tree-based programs, into LCSs could provide advances in scaling. However, since solving hard problems often requires constructing high-level building blocks, which also results in an intractable search space, a limit of scaling will eventually be reached. Inspired by human problem-solving abilities, XCSCF* can reuse learned knowledge and learned functionality to scale to complex problems by transferring them from simpler problems using layered learning. However, this method was unrefined and suited to only the Multiplexer problem domain. In this paper, we propose improvements to XCSCF* to enable it to be robust across multiple problem domains. This is demonstrated on the benchmarks Multiplexer, Carry-one, Majority-on, and Even-parity domains. The required base axioms necessary for learning are proposed, methods for transfer learning in LCSs developed and learning recast as a decomposition into a series of subordinate problems. Results show that from a conventional tabula rasa, with only a vague notion of what subordinate problems might be relevant, it is possible to capture the general logic behind the tested domains, so the advanced system is capable of solving any individual n-bit Multiplexer, n-bit Carry-one, n-bit Majority-on, or n-bit Even-parity problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge