A Group Theoretic Metric for Robot State Estimation Leveraging Chebyshev Interpolation

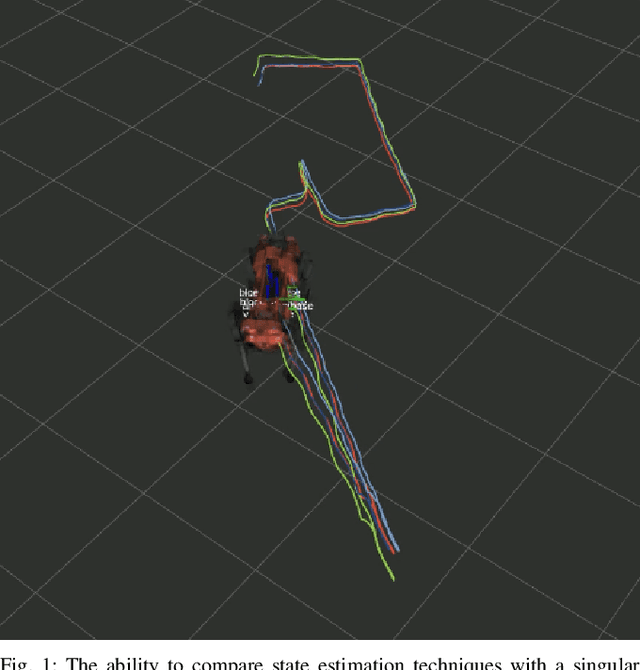
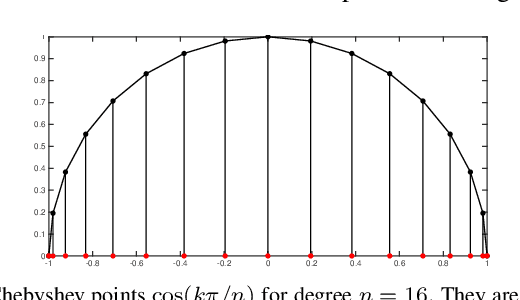
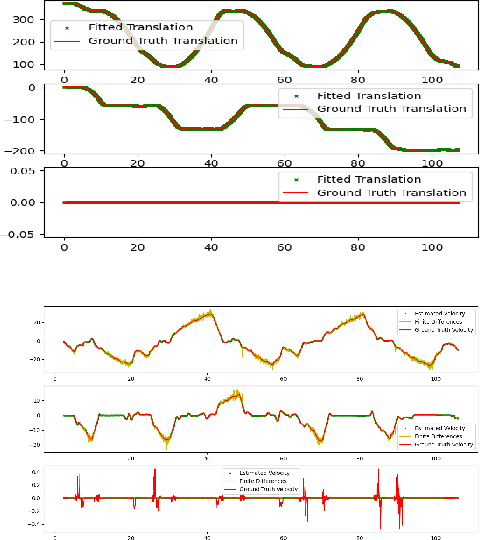
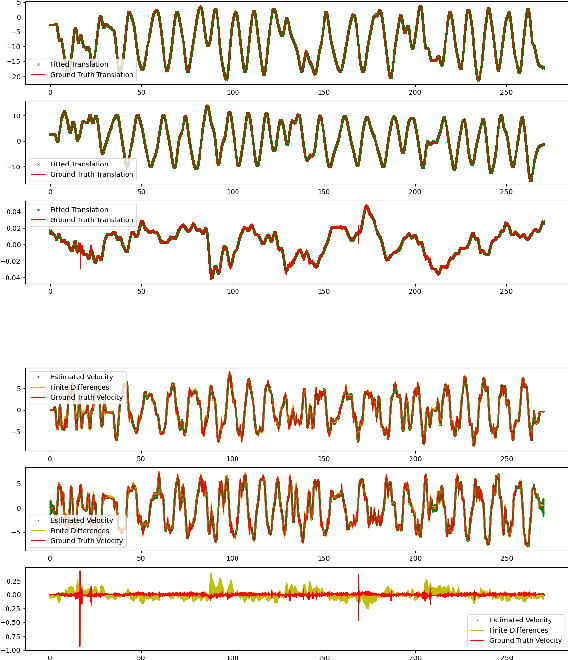
We propose a new metric for robot state estimation based on the recently introduced $\text{SE}_2(3)$ Lie group definition. Our metric is related to prior metrics for SLAM but explicitly takes into account the linear velocity of the state estimate, improving over current pose-based trajectory analysis. This has the benefit of providing a single, quantitative metric to evaluate state estimation algorithms against, while being compatible with existing tools and libraries. Since ground truth data generally consists of pose data from motion capture systems, we also propose an approach to compute the ground truth linear velocity based on polynomial interpolation. Using Chebyshev interpolation and a pseudospectral parameterization, we can accurately estimate the ground truth linear velocity of the trajectory in an optimal fashion with best approximation error. We demonstrate how this approach performs on multiple robotic platforms where accurate state estimation is vital, and compare it to alternative approaches such as finite differences. The pseudospectral parameterization also provides a means of trajectory data compression as an additional benefit. Experimental results show our method provides a valid and accurate means of comparing state estimation systems, which is also easy to interpret and report.