A Graduated Filter Method for Large Scale Robust Estimation
Paper and Code
Mar 20, 2020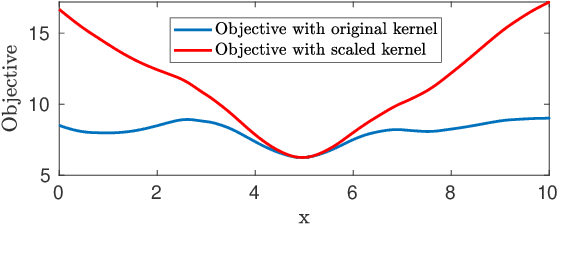
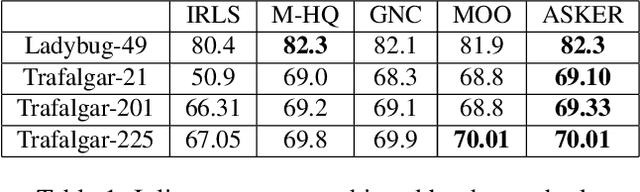
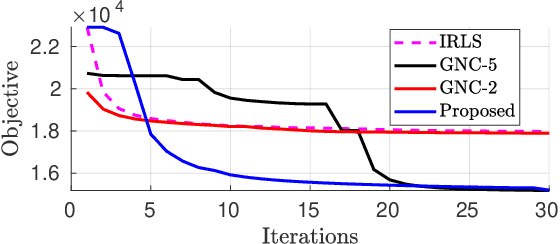
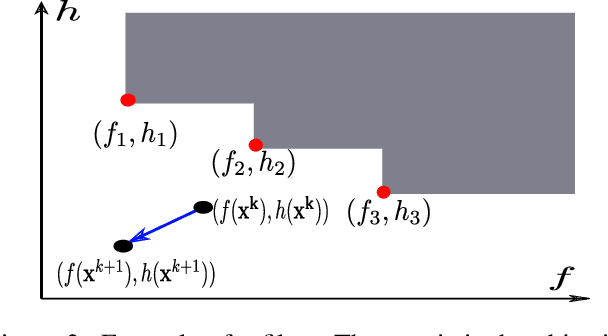
Due to the highly non-convex nature of large-scale robust parameter estimation, avoiding poor local minima is challenging in real-world applications where input data is contaminated by a large or unknown fraction of outliers. In this paper, we introduce a novel solver for robust estimation that possesses a strong ability to escape poor local minima. Our algorithm is built upon the class of traditional graduated optimization techniques, which are considered state-of-the-art local methods to solve problems having many poor minima. The novelty of our work lies in the introduction of an adaptive kernel (or residual) scaling scheme, which allows us to achieve faster convergence rates. Like other existing methods that aim to return good local minima for robust estimation tasks, our method relaxes the original robust problem but adapts a filter framework from non-linear constrained optimization to automatically choose the level of relaxation. Experimental results on real large-scale datasets such as bundle adjustment instances demonstrate that our proposed method achieves competitive results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge