A Generative Model for Molecular Distance Geometry
Paper and Code
Oct 03, 2019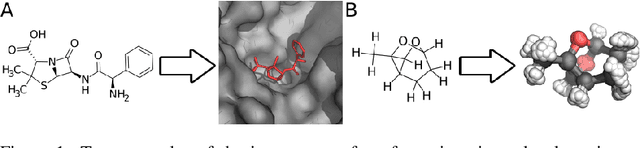


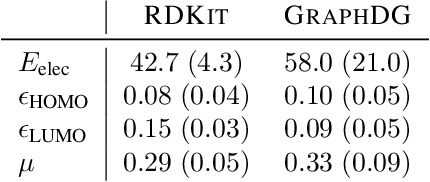
Computing equilibrium states for many-body systems, such as molecules, is a long-standing challenge. In the absence of methods for generating statistically independent samples, great computational effort is invested in simulating these systems using, for example, Markov chain Monte Carlo. We present a probabilistic model that generates such samples for molecules from their graph representations. Our model learns a low-dimensional manifold that preserves the geometry of local atomic neighborhoods through a principled learning representation that is based on Euclidean distance geometry. We create a new dataset for molecular conformation generation with which we show experimentally that our generative model achieves state-of-the-art accuracy. Finally, we show how to use our model as a proposal distribution in an importance sampling scheme to compute molecular properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge