A Generally Applicable, Highly Scalable Measurement Computation and Optimization Approach to Sequential Model-Based Diagnosis
Paper and Code
Nov 15, 2017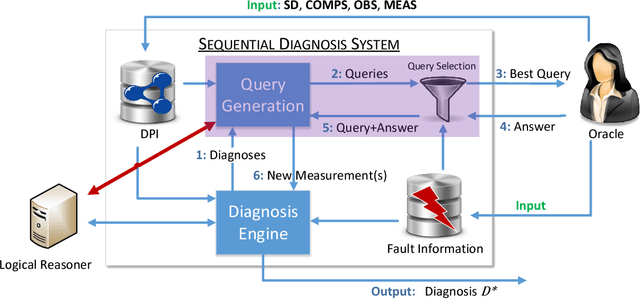



Model-Based Diagnosis deals with the identification of the real cause of a system's malfunction based on a formal system model and observations of the system behavior. When a malfunction is detected, there is usually not enough information available to pinpoint the real cause and one needs to discriminate between multiple fault hypotheses (called diagnoses). To this end, Sequential Diagnosis approaches ask an oracle for additional system measurements. This work presents strategies for (optimal) measurement selection in model-based sequential diagnosis. In particular, assuming a set of leading diagnoses being given, we show how queries (sets of measurements) can be computed and optimized along two dimensions: expected number of queries and cost per query. By means of a suitable decoupling of two optimizations and a clever search space reduction the computations are done without any inference engine calls. For the full search space, we give a method requiring only a polynomial number of inferences and show how query properties can be guaranteed which existing methods do not provide. Evaluation results using real-world problems indicate that the new method computes (virtually) optimal queries instantly independently of the size and complexity of the considered diagnosis problems and outperforms equally general methods not exploiting the proposed theory by orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge