A Generalized Bootstrap Target for Value-Learning, Efficiently Combining Value and Feature Predictions
Paper and Code
Jan 05, 2022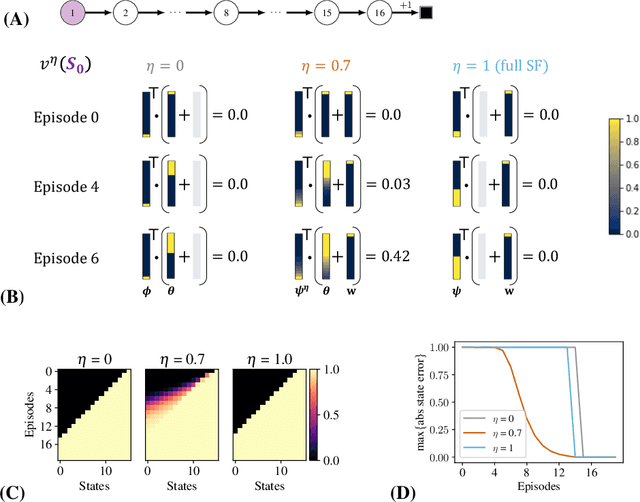



Estimating value functions is a core component of reinforcement learning algorithms. Temporal difference (TD) learning algorithms use bootstrapping, i.e. they update the value function toward a learning target using value estimates at subsequent time-steps. Alternatively, the value function can be updated toward a learning target constructed by separately predicting successor features (SF)--a policy-dependent model--and linearly combining them with instantaneous rewards. We focus on bootstrapping targets used when estimating value functions, and propose a new backup target, the $\eta$-return mixture, which implicitly combines value-predictive knowledge (used by TD methods) with (successor) feature-predictive knowledge--with a parameter $\eta$ capturing how much to rely on each. We illustrate that incorporating predictive knowledge through an $\eta\gamma$-discounted SF model makes more efficient use of sampled experience, compared to either extreme, i.e. bootstrapping entirely on the value function estimate, or bootstrapping on the product of separately estimated successor features and instantaneous reward models. We empirically show this approach leads to faster policy evaluation and better control performance, for tabular and nonlinear function approximations, indicating scalability and generality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge