A Generalised Inverse Reinforcement Learning Framework
Paper and Code
May 25, 2021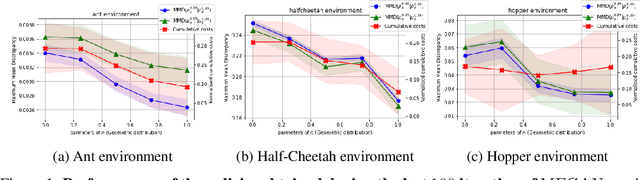
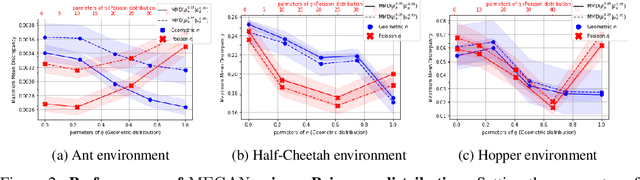
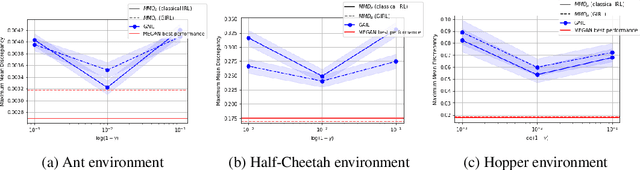
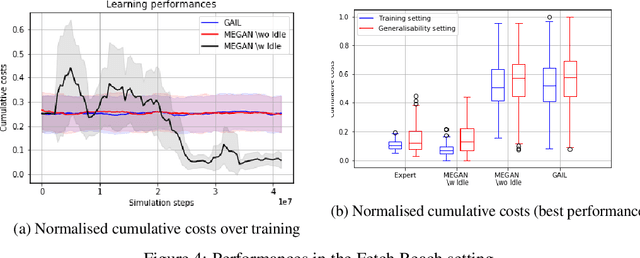
The gloabal objective of inverse Reinforcement Learning (IRL) is to estimate the unknown cost function of some MDP base on observed trajectories generated by (approximate) optimal policies. The classical approach consists in tuning this cost function so that associated optimal trajectories (that minimise the cumulative discounted cost, i.e. the classical RL loss) are 'similar' to the observed ones. Prior contributions focused on penalising degenerate solutions and improving algorithmic scalability. Quite orthogonally to them, we question the pertinence of characterising optimality with respect to the cumulative discounted cost as it induces an implicit bias against policies with longer mixing times. State of the art value based RL algorithms circumvent this issue by solving for the fixed point of the Bellman optimality operator, a stronger criterion that is not well defined for the inverse problem. To alleviate this bias in IRL, we introduce an alternative training loss that puts more weights on future states which yields a reformulation of the (maximum entropy) IRL problem. The algorithms we devised exhibit enhanced performances (and similar tractability) than off-the-shelf ones in multiple OpenAI gym environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge