A General Machine Learning Framework for Survival Analysis
Paper and Code
Jun 27, 2020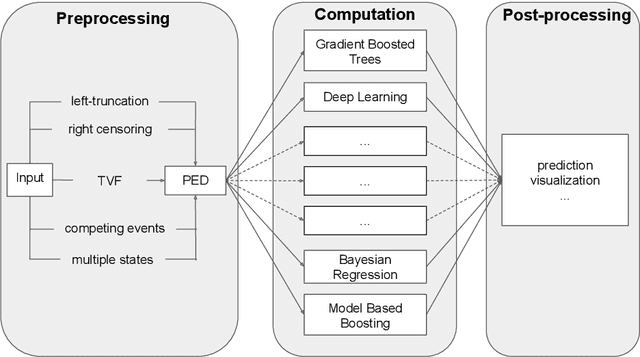

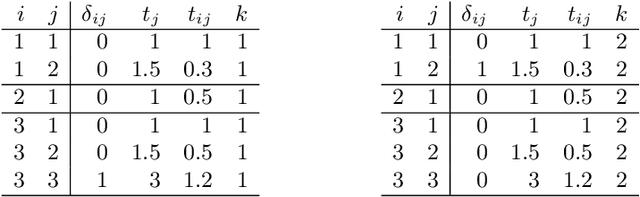
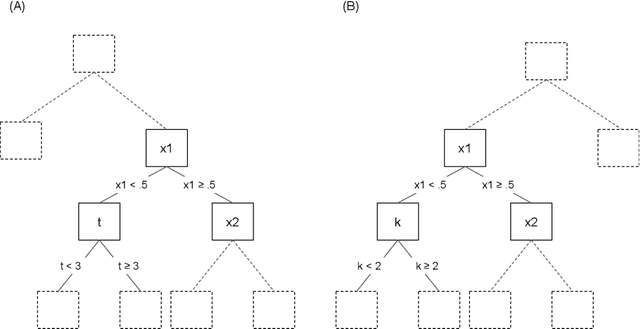
The modeling of time-to-event data, also known as survival analysis, requires specialized methods that can deal with censoring and truncation, time-varying features and effects, and that extend to settings with multiple competing events. However, many machine learning methods for survival analysis only consider the standard setting with right-censored data and proportional hazards assumption. The methods that do provide extensions usually address at most a subset of these challenges and often require specialized software that can not be integrated into standard machine learning workflows directly. In this work, we present a very general machine learning framework for time-to-event analysis that uses a data augmentation strategy to reduce complex survival tasks to standard Poisson regression tasks. This reformulation is based on well developed statistical theory. With the proposed approach, any algorithm that can optimize a Poisson (log-)likelihood, such as gradient boosted trees, deep neural networks, model-based boosting and many more can be used in the context of time-to-event analysis. The proposed technique does not require any assumptions with respect to the distribution of event times or the functional shapes of feature and interaction effects. Based on the proposed framework we develop new methods that are competitive with specialized state of the art approaches in terms of accuracy, and versatility, but with comparatively small investments of programming effort or requirements for specialized methodological know-how.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge