A general framework for label-efficient online evaluation with asymptotic guarantees

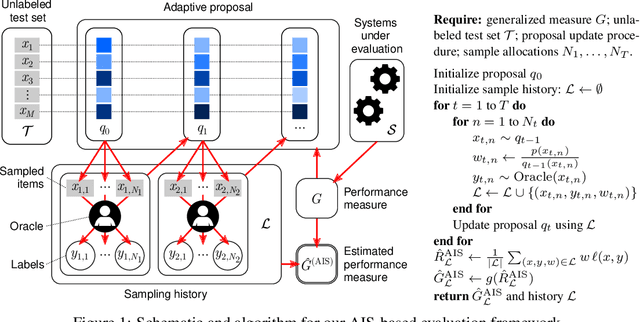
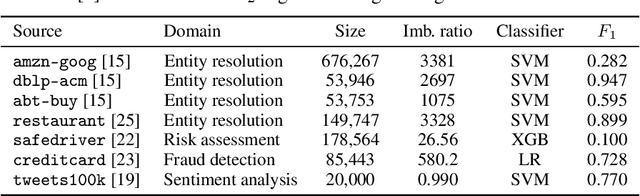
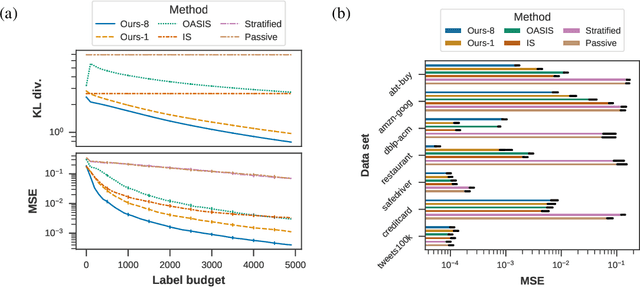
Achieving statistically significant evaluation with passive sampling of test data is challenging in settings such as extreme classification and record linkage, where significant class imbalance is prevalent. Adaptive importance sampling focuses labeling on informative regions of the instance space, however it breaks data independence assumptions - commonly required for asymptotic guarantees that assure estimates approximate population performance and provide practical confidence intervals. In this paper we develop an adaptive importance sampling framework for supervised evaluation that defines a sequence of proposal distributions given a user-defined discriminative model of p(y|x) and a generalized performance measure to evaluate. Under verifiable conditions on the model and performance measure, we establish strong consistency and a (martingale) central limit theorem for resulting performance estimates. We instantiate our framework with worked examples given stochastic or deterministic label oracle access. Both examples leverage Dirichlet-tree models for practical online evaluation, with the deterministic case achieving asymptotic optimality. Experiments on seven datasets demonstrate an average mean-squared error superior to state-of-the-art samplers on fixed label budgets.