A General Approach to Domain Adaptation with Applications in Astronomy
Paper and Code
Dec 20, 2018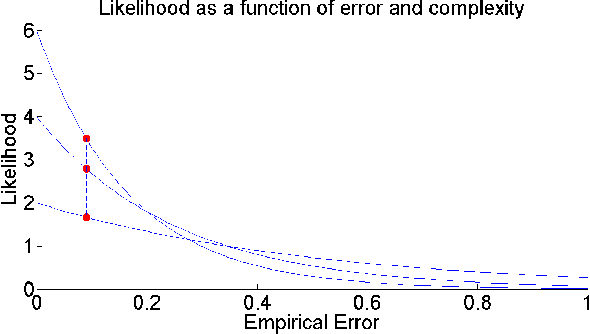
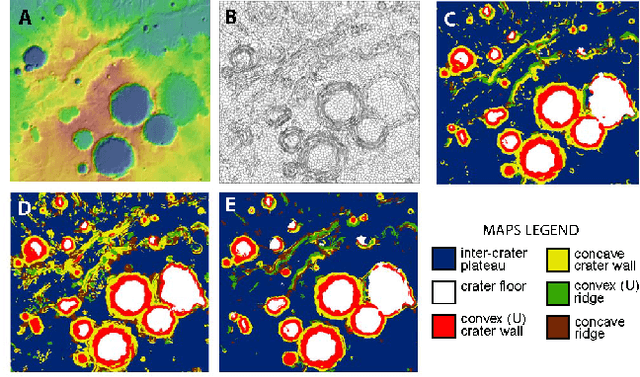
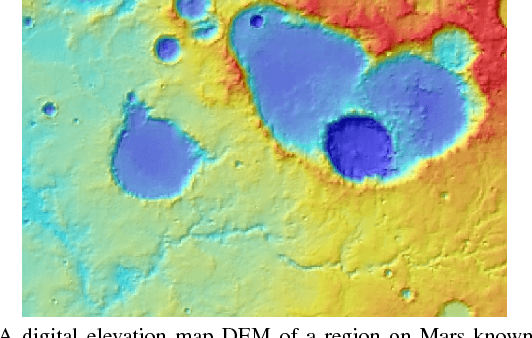
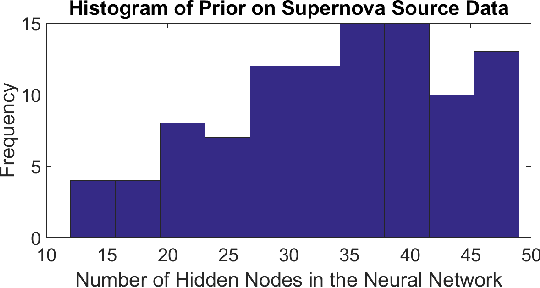
The ability to build a model on a source task and subsequently adapt such model on a new target task is a pervasive need in many astronomical applications. The problem is generally known as transfer learning in machine learning, where domain adaptation is a popular scenario. An example is to build a predictive model on spectroscopic data to identify Supernovae IA, while subsequently trying to adapt such model on photometric data. In this paper we propose a new general approach to domain adaptation that does not rely on the proximity of source and target distributions. Instead we simply assume a strong similarity in model complexity across domains, and use active learning to mitigate the dependency on source examples. Our work leads to a new formulation for the likelihood as a function of empirical error using a theoretical learning bound; the result is a novel mapping from generalization error to a likelihood estimation. Results using two real astronomical problems, Supernova Ia classification and identification of Mars landforms, show two main advantages with our approach: increased accuracy performance and substantial savings in computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge