A Fourier Approach to the Parameter Estimation Problem for One-dimensional Gaussian Mixture Models
Paper and Code
Apr 19, 2024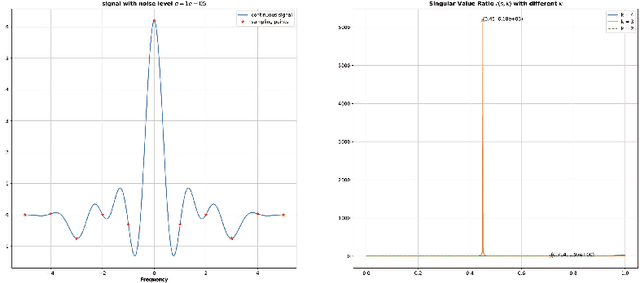
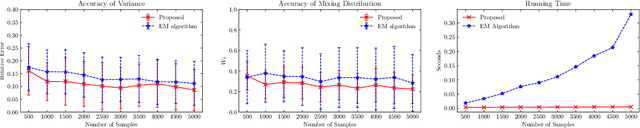

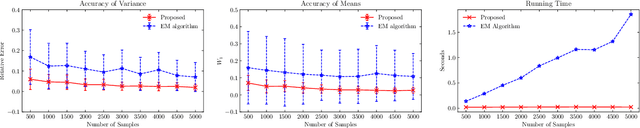
The purpose of this paper is twofold. First, we propose a novel algorithm for estimating parameters in one-dimensional Gaussian mixture models (GMMs). The algorithm takes advantage of the Hankel structure inherent in the Fourier data obtained from independent and identically distributed (i.i.d) samples of the mixture. For GMMs with a unified variance, a singular value ratio functional using the Fourier data is introduced and used to resolve the variance and component number simultaneously. The consistency of the estimator is derived. Compared to classic algorithms such as the method of moments and the maximum likelihood method, the proposed algorithm does not require prior knowledge of the number of Gaussian components or good initial guesses. Numerical experiments demonstrate its superior performance in estimation accuracy and computational cost. Second, we reveal that there exists a fundamental limit to the problem of estimating the number of Gaussian components or model order in the mixture model if the number of i.i.d samples is finite. For the case of a single variance, we show that the model order can be successfully estimated only if the minimum separation distance between the component means exceeds a certain threshold value and can fail if below. We derive a lower bound for this threshold value, referred to as the computational resolution limit, in terms of the number of i.i.d samples, the variance, and the number of Gaussian components. Numerical experiments confirm this phase transition phenomenon in estimating the model order. Moreover, we demonstrate that our algorithm achieves better scores in likelihood, AIC, and BIC when compared to the EM algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge